Mấy b n làm bài này mik cái. Mik đag cần gấp.
n làm bài này mik cái. Mik đag cần gấp.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1. I enjoy playing sports because it is good for my health
2. Do your children go camping every summer holiday?
3. I think photography can be an expensive hobby.
4. My cousin will give me a book as a gift on my next birthday.
5. He finds mountain climbing dangerous so he doesn't take it
6. I hope in the future he will teach me how to do eggshell carving.
1. I enjoy playing sports because it's good for health.
2.Does your children go camping every summer holiday?
3.I think photography can be a expensive hobby
4.My cousin gives me a book to gift my next birth day
5.He finds mountain climbing dangerous, so he doesn't take it.
6.I hope in the future, he will teach me how to do eggshell carving
----Cái này mk tự làm nên ko chắc là đúng đâu nhé----

c, \(C=\left(2\sqrt{3}-5\sqrt{27}+4\sqrt{12}\right):\sqrt{3}\)
<=> \(C=\left(2\sqrt{3}-15\sqrt{3}+8\sqrt{3}\right):\sqrt{3}\)
<=> \(C=-5\sqrt{3}:\sqrt{3}=-5\)
e. \(\left(\sqrt{3-\sqrt{5}}+\sqrt{3+\sqrt{5}}\right)^2\)
\(=3-\sqrt{5}+3+\sqrt{5}+2\sqrt{\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)}\)
\(=6+2\sqrt{9-5}\)
\(=6+4=10\)
b. \(\left(\sqrt{3}+2\right)^2-\sqrt{75}\)
\(=3+4\sqrt{3}+4-5\sqrt{3}\)
\(=7-\sqrt{3}\)
d. \(\left(1+\sqrt{3}-\sqrt{2}\right)\left(1+\sqrt{3}+\sqrt{2}\right)\)
\(=\left(1+\sqrt{3}\right)^2-2\)
\(=1+2\sqrt{3}+3-2\)
\(=2+2\sqrt{3}\)
f. \(\sqrt{\left(\sqrt{3}+2\right)^2}-\sqrt{\left(\sqrt{3}-2\right)^2}\)
\(=\left|\sqrt{3}+2\right|-\left|\sqrt{3}-2\right|\)
\(=\sqrt{3}+2-2+\sqrt{3}\)
\(=2\sqrt{3}\)
c: Ta có: \(C=\left(2\sqrt{3}-5\sqrt{27}+4\sqrt{12}\right):\sqrt{3}\)
\(=\left(2\sqrt{3}-5\cdot3\sqrt{3}+4\cdot2\sqrt{3}\right):\sqrt{3}\)
\(=2-15+8=-5\)
d: Ta có: \(D=\left(\sqrt{3-\sqrt{5}}+\sqrt{3+\sqrt{5}}\right)^2\)
\(=3-\sqrt{5}+3+\sqrt{5}+2\cdot\sqrt{\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)}\)
\(=6+2\cdot2=10\)

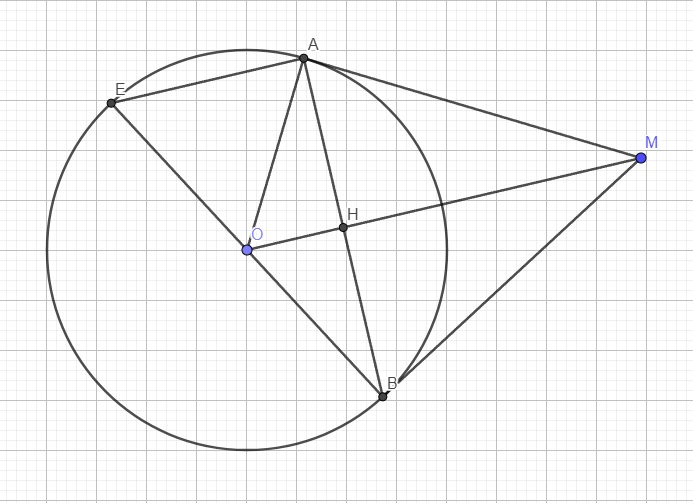
1: Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
=>CE\(\perp\)AB tại E
Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do đó: ΔBDC vuông tại D
=>BD\(\perp\)AC tại D
Xét ΔABC có
BD,CE là các đường cao
BD cắt CE tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC tại F
2: Xét ΔFBH vuông tại F và ΔFAC vuông tại F có
\(\widehat{FBH}=\widehat{FAC}\left(=90^0-\widehat{ACF}\right)\)
Do đó: ΔFBH~ΔFAC
=>\(\dfrac{FB}{FA}=\dfrac{FH}{FC}\)
=>\(FB\cdot FC=FA\cdot FH\)
3: Xét tứ giác AEHD có
\(\widehat{AEH}+\widehat{ADH}=90^0+90^0=180^0\)
nên AEHD là tứ giác nội tiếp đường tròn đường kính AH
Tâm I là trung điểm của AH

a.
Do MA là tiếp tuyến tại A \(\Rightarrow MA\perp OA\Rightarrow\widehat{MAO}=90^0\)
Xét hai tam giác OMA và OMB có:
\(\left\{{}\begin{matrix}OA=OB=R\\MA=MB\left(gt\right)\\OM\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta OMA=\Delta OMB\left(c.c.c\right)\)
\(\Rightarrow\widehat{MBO}=\widehat{MAO}=90^0\)
\(\Rightarrow MB\perp OB\Rightarrow MB\) là tiếp tuyến
b.
Gọi H là giao điểm AB và OM
Ta có: \(\left\{{}\begin{matrix}OA=OB=R\\MA=MB\left(gt\right)\end{matrix}\right.\) \(\Rightarrow OM\) là trung trực AB
\(\Rightarrow OM\perp AB\) tại H đồng thời \(HA=HB=\dfrac{AB}{2}\)
Trong tam giác vuông OMA: \(cos\widehat{AOM}=\dfrac{OA}{OM}=\dfrac{2}{2R}=\dfrac{1}{2}\Rightarrow\widehat{AOM}=60^0\)
\(\Rightarrow\widehat{AMO}=90^0-\widehat{AOM}=30^0\)
\(\Rightarrow\widehat{AMB}=2\widehat{AMO}=60^0\)
\(\Rightarrow\Delta AMB\) đều (tam giác cân có 1 góc bằng 60 độ)
Trong tam giác vuông OAH:
\(AH=OA.sin\widehat{AOM}=R.sin60^0=\dfrac{R\sqrt{3}}{3}\)
\(\Rightarrow AB=2AH=R\sqrt{3}\)
\(OH=OA.cos\widehat{AOM}=R.cos30^0=\dfrac{R}{2}\)
\(\Rightarrow HM=OM-OH=\dfrac{3R}{2}\)
\(\Rightarrow S_{ABM}=\dfrac{1}{2}HM.AB=\dfrac{3R^2\sqrt{3}}{4}\)
c.
BE là đường kính \(\Rightarrow\widehat{BAE}\) là góc nt chắn nửa đường tròn
\(\Rightarrow\widehat{BAE}=90^0\Rightarrow AB\perp AE\)
Mà \(AB\perp OM\) (theo cm câu b)
\(\Rightarrow AE||OM\) (cùng vuông góc AB)


29: Ta có: \(\dfrac{1}{\sqrt{7}+\sqrt{5}}+\dfrac{2}{1-\sqrt{7}}\)
\(=\dfrac{\sqrt{7}-\sqrt{5}}{2}-\dfrac{2\sqrt{7}-2}{6}\)
\(=\dfrac{3\sqrt{7}-3\sqrt{5}-2\sqrt{7}+2}{6}\)
\(=\dfrac{-3\sqrt{5}-2}{6}\)
30: Ta có: \(\dfrac{4}{1-\sqrt{3}}+\dfrac{\sqrt{3}-1}{\sqrt{3}+1}\)
\(=\dfrac{-4\sqrt{3}-4}{2}+\dfrac{4-2\sqrt{3}}{2}\)
\(=\dfrac{-4\sqrt{3}-4+4-2\sqrt{3}}{2}=-3\sqrt{3}\)
31: Ta có: \(\dfrac{1}{\sqrt{2}-\sqrt{3}}-\dfrac{3}{\sqrt{18}+2\sqrt{3}}\)
\(=-\sqrt{3}-\sqrt{2}-\dfrac{3}{3\sqrt{2}+2\sqrt{3}}\)
\(=-\sqrt{3}-\sqrt{2}-\dfrac{9\sqrt{2}-6\sqrt{3}}{6}\)
\(=\dfrac{-6\sqrt{3}-6\sqrt{2}-9\sqrt{2}+6\sqrt{3}}{6}=\dfrac{-15\sqrt{2}}{6}\)
\(=\dfrac{-5\sqrt{2}}{2}\)
29.
\(=\frac{\sqrt{7}-\sqrt{5}}{(\sqrt{7}-\sqrt{5})(\sqrt{7}+\sqrt{5})}+\frac{2(1+\sqrt{7})}{(1-\sqrt{7})(1+\sqrt{7})}\)
\(=\frac{\sqrt{7}-\sqrt{5}}{7-5}+\frac{2(1+\sqrt{7})}{1-7}=\frac{\sqrt{7}-\sqrt{5}}{2}-\frac{1+\sqrt{7}}{3}=\frac{\sqrt{7}-3\sqrt{5}-2}{6}\)



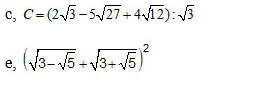
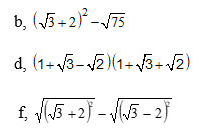 các bạn giải hộ mik mấy câu này vs mik đag cần gấp
các bạn giải hộ mik mấy câu này vs mik đag cần gấp


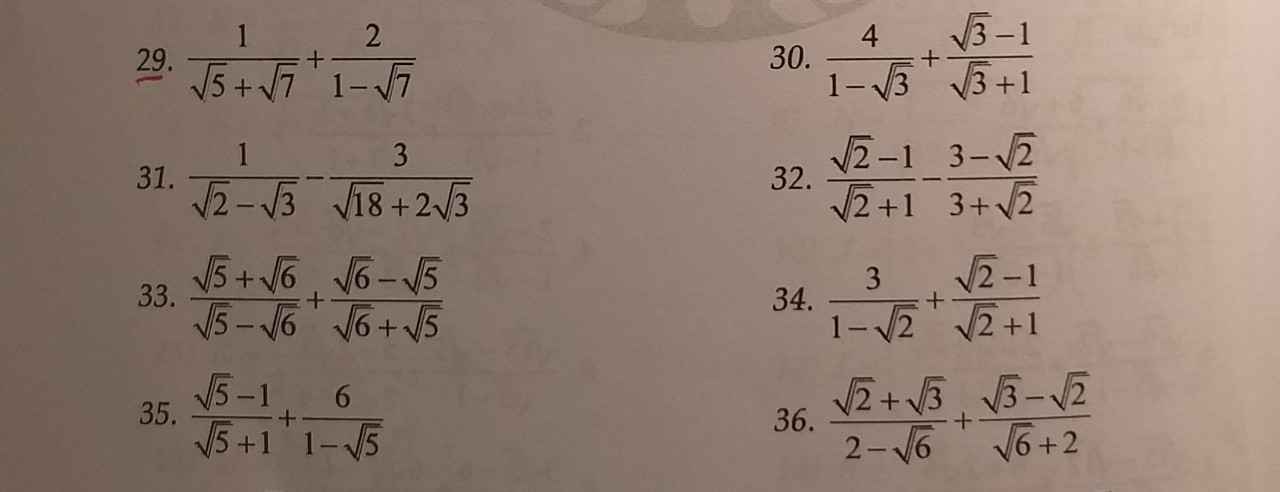
Em có cảm xúc khi nghe bài hát trên là: xúc động, vui vẻ, hạnh phúc và hài lòng.
-Nội dung bài hát thể hiện tình yêu thương của con người đối với mọi người xung quanh.
Mình không biết có đúng ko nữa, nếu sai thì mong bạn thông cảm!
Người viết
Hạ
Đàm Xuân Hạ lớp 7a trường THCS Lạc Đạo