Chỉ giúp em mấy câu này vs
Em cảm ơn nhiều .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LT
28 tháng 8 2021
17. Despite promising that he wouldn't be late, he didn't arrive until 9 o'clock.
18. I didn't use to listen to Western music some years ago.
19. My mum used to be a chef in Cham restaurant, but now he is retired.
20. There used to be a market here in 2003.
21. The new restaurant looks good. However, it seems to have few customers.
22. They didn't use to know how to drive a car, but now they can drive well.
23. We planned to visit Petronas in the afternoon. However, we couldn't afford the fee.
24. Despite being sick, Marry didn't leave the meeting until it ended.
25. There used to be less vehicles on the roads in the past.
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 9 2021
3.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
B đúng
4.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(0;1\right)\)
A đúng
1.
B sai (thiếu điều kiện \(f'\left(x\right)=0\) tại hữu hạn điểm)
NH
2
TN
1
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 8 2021
Do MN là đường trung bình tam giác ABC \(\Rightarrow MN||AB\) mà \(AB||CD\Rightarrow MN||CD\)
MN và (ABCD) không có điểm chung \(\Rightarrow MN||\left(ABCD\right)\)
MN và (SCD) không có điểm chung \(\Rightarrow MN||\left(SCD\right)\)
MN nằm trên (SAB) nên MN không song song (SAB)
Vậy MN song song với cả (ABCD) và (SCD)
V
0
TP
22 tháng 7 2021
a ) H2SO4 + 2NaOH ----------> Na2SO4 + H2O
H2SO4 + 2NaHCO3 ----------> Na2SO4 + 2H2O + 2CO2
\(n_{H_2SO_4}=0,5a\)
\(n_{NaOH}=0,2.2=0,4\left(mol\right)\)
\(n_{NaHCO_3}=\dfrac{0,42}{84}=0,005\left(mol\right)\)
Trường hợp 1: H2SO4 dư
H2SO4 + 2NaOH ----------> Na2SO4 + H2O
0,2<---------0,4
nH2SO4dư = 0,5a - 0,2 (mol)
=> \(\dfrac{1}{2}n_{H_2SO_4}=0,25a-0,1\left(mol\right)\)
H2SO4 + 2NaHCO3 ----------> Na2SO4 + 2H2O + 2CO2
\(n_{H_2SO_4\left(dư\right)}=\dfrac{1}{2}n_{NaHCO_3}=0,0025\left(mol\right)\)
=> \(0,25.a-0,1=0,0025\)
=> a=0,41 (M)
Trường hợp 2: NaOH dư
H2SO4 + 2NaOH -----> K2SO4 + 2H2O
0,5a-------->a
nNaOHdư = 0.4 - a (mol)
=> \(\dfrac{1}{2}n_{NaOH\left(dư\right)}=0,2-0,5a\left(mol\right)\)
NaHCO3 + NaOH -------> Na2CO3 + H2O
0,005-------->0,005
=> 0,2 - 0.5a = 0,005
=> a = 0,39
TP
gấp mn giúp em câu này vs ạ e gấp lắm mn giúp em vs em cảm ơn ạ
0
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 1 2022
Chắc đề đúng là \(\dfrac{1}{4+1^4}+\dfrac{3}{4+3^4}+...\)
- Với \(n=1\) đẳng thức đúng
- Giả sử đẳng thức cũng đúng với \(n=k>1\) hay:
\(\dfrac{1}{4+1^4}+\dfrac{3}{4+3^4}+...+\dfrac{2k-1}{4+\left(2k-1\right)^4}=\dfrac{k^2}{4k^2+1}\)
- Ta cần chứng minh nó cũng đúng với \(n=k+1\) hay:
\(\dfrac{1}{4+1^4}+\dfrac{3}{4+3^4}+...+\dfrac{2k-1}{4+\left(2k-1\right)^4}+\dfrac{2k+1}{4+\left(2k+1\right)^4}=\dfrac{\left(k+1\right)^2}{4\left(k+1\right)^2+1}\)
Thật vậy, ta có:
\(\dfrac{1}{4+1^4}+\dfrac{3}{4+3^4}+...+\dfrac{2k-1}{4+\left(2k-1\right)^4}+\dfrac{2k+1}{4+\left(2k+1\right)^4}=\dfrac{k^2}{4k^2+1}+\dfrac{2k+1}{4+\left(2k+1\right)^4}\)
\(=\dfrac{k^2}{4k^2+1}+\dfrac{2k+1}{\left(2k+1\right)^4+4\left(2k+1\right)^2+4-4\left(2k+1\right)^2}=\dfrac{k^2}{4k^2+1}+\dfrac{2k+1}{\left(4k^2+4k+3\right)^2-\left(4k+2\right)^2}\)
\(=\dfrac{k^2}{4k^2+1}+\dfrac{2k+1}{\left(4k^2+1\right)\left(4k^2+8k+5\right)}=\dfrac{k^2\left(4k^2+8k+5\right)+2k+1}{\left(4k^2+1\right)\left(4k^2+8k+5\right)}\)
\(=\dfrac{\left(k+1\right)^2\left(4k^2+1\right)}{\left(4k^2+1\right)\left(4k^2+8k+5\right)}=\dfrac{\left(k+1\right)^2}{4k^2+8k+5}=\dfrac{\left(k+1\right)^2}{4\left(k+1\right)^2+1}\) (đpcm)
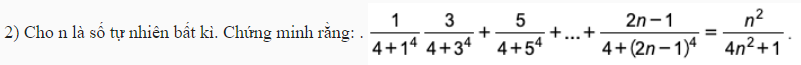
1. If you are calm, you won't make a wrong decision.
2. These wonderful poems were written by a great poet.
3.Because of rained heavily, Jane didn't go fishing yesterday.
4.Vietnamese people use Khue Van pavilion as a symbol of Hanoi.
5. His idea is not the same as me.
6. Those modern paintings are not as expensive as these Dong Ho paintings.
7. What food do you like?
8.These machines are used by chefs to mix the ingredients.
9. It i've most seen such a boring movie.
10. There are not many eggs in the fridge.
11.They started living there 2 years ago.
12. I have never drunk cocktail before.
13.This exercise is not as difficult as the last one.
14. I find playing computer games boring.
15. The new building has the same height as the old one.
16. She didn't have enough eggs to make an omelette.
17. In spite of promising that wouldn't be late, he didn't arrive until 9 o'clock.
18. I didn't use to listen to Western music some years ago.
19. My mum used to be a chef in Cham restaurant, but now she is tired.