Xét một cách quạt đang quay tròn đều nếu một điểm trên cánh quạt dịch khỏi vị trí cũ 20 cm thì tóc độ dài của cánh quạt tăng gấp 3 lần. Ban đầu điểm đó cách trục quay của cánh quạt là bao nhiêu ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Một cánh quạt dài 50 cm đang quay đều với tốc độ gócπrad/s. Tốc độ dài của một điểm ở đầu cánh quạt là A. 157 cm/s. B. 100 cm/s. C. 50 cm/s. D. 25 cm/s.
Tóm tắt: \(R=50cm=0,5m;\omega=\pi\)(rad/s)
\(v=?\)
Bài giải:
Tốc độ dài của vật:
\(v=R\cdot\omega=0,5\cdot\pi=\dfrac{1}{2}\pi\approx1,57\)m/s=157cm/s
Chọn A.

Một quạt máy quay với tần số 450/ vòng/phút cánh quạt dài 0,8 m. Tính;tốc độ góc tốc độ dài của một điểm ở đầu cánh quạt

Theo công thức tính chu vi đường tròn có bán kính R, ta có chiều dài của nửa đường tròn bằng πR.
Vì cung tròn của đường tròn có chiều dài là R tương ứng với góc 1 rad nên chiều dài tương ứng với góc π rad.

\(F=360\left(\dfrac{vòng}{ph}\right)=6\left(\dfrac{vòng}{s}\right)\)
\(R=60cm=0,6m\)
Chu kì quay của cánh quạt: \(T=\dfrac{1}{f}=\dfrac{1}{6}s\)
Tốc độ góc: \(\omega=\dfrac{2\pi}{T}=\dfrac{2\pi}{\dfrac{1}{6}}=12\pi\left(\dfrac{rad}{s}\right)\)
Tốc độ dài là: \(v=\omega.R=12\pi.0,6=7,2\pi\left(\dfrac{m}{s}\right)\)
Gia tốc hướng tâm: \(a_{ht}=R.\omega^2=0,6.\left(12\pi\right)^2\approx851,87\left(\dfrac{m}{s^2}\right)\)

Theo công thức tính chu vi đường tròn có bán kính R, ta có chiều dài của nửa đường tròn bằng πR.
Vì cung tròn của đường tròn có chiều dài là R tương ứng với góc 1 rad nên chiều dài tương ứng với góc π rad.

Ta có:
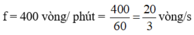
Tốc độ góc của một điểm bất kì ở đầu cánh quạt là:
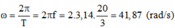
Tốc độ dài của điểm trên đầu cánh quạt là: V = R.ω = 33,5 m/s.
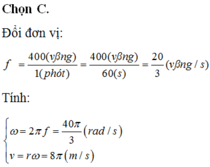
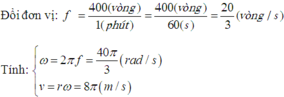
Gọi a độ dài từ điểm chấm đền trục quay của cánh quạt
Vì khi dịch chuyển đi 20cm thì tốc độ tăng gấp 3 lần
=> Bán kính sau là: a - 0,2 (m)
Ta có: \(v_1=3v_2\)
\(\Leftrightarrow a.\omega=3\left(a-0,2\right).\omega\)
\(\Rightarrow a=0,3\left(m\right)\)