1) Cho tỉ lệ thức \(\dfrac{a}{b}=\dfrac{c}{d}\). CMR(với giả thiết các tỉ số đều có nghĩa)
a)\(\dfrac{a-b}{a+b}=\dfrac{c-d}{c+d}\)
b)\(\dfrac{ab}{cd}=\dfrac{\left(a-b\right)^2}{\left(c-d\right)^2}\)
c)\(\dfrac{2a+5b}{3a-4b}=\dfrac{2c+5d}{3c-4d}\)
2) Cho tỉ lệ thức \(\dfrac{a}{b}=\dfrac{c}{d}\). CMR ta có các tỉ lệ thức sau
a)\(\dfrac{a}{a+b}=\dfrac{c}{c+d}\)
b)\(\dfrac{7a1^2+5ac}{7a^2-5ac}=\dfrac{7b^2+5bd}{7b^2-5bd}\)
3) CMR nếu \(a^2=bc\) thì \(\dfrac{a+b}{a-b}=\dfrac{c+a}{c-a}\). Đảo lại có đúng không?
4) CMR nếu \(\dfrac{a}{b}=\dfrac{b}{d}\) thì \(\dfrac{a^2+b^2}{b^2+d^2}=\dfrac{a}{d}\)
5) Cho tỉ lệ thức \(\dfrac{a^2+b^2}{c^2+d^2}=\dfrac{ab}{cd}.CMR\dfrac{a}{b}=\dfrac{c}{d}\)
các bn giúp bn Heo Mách với nha

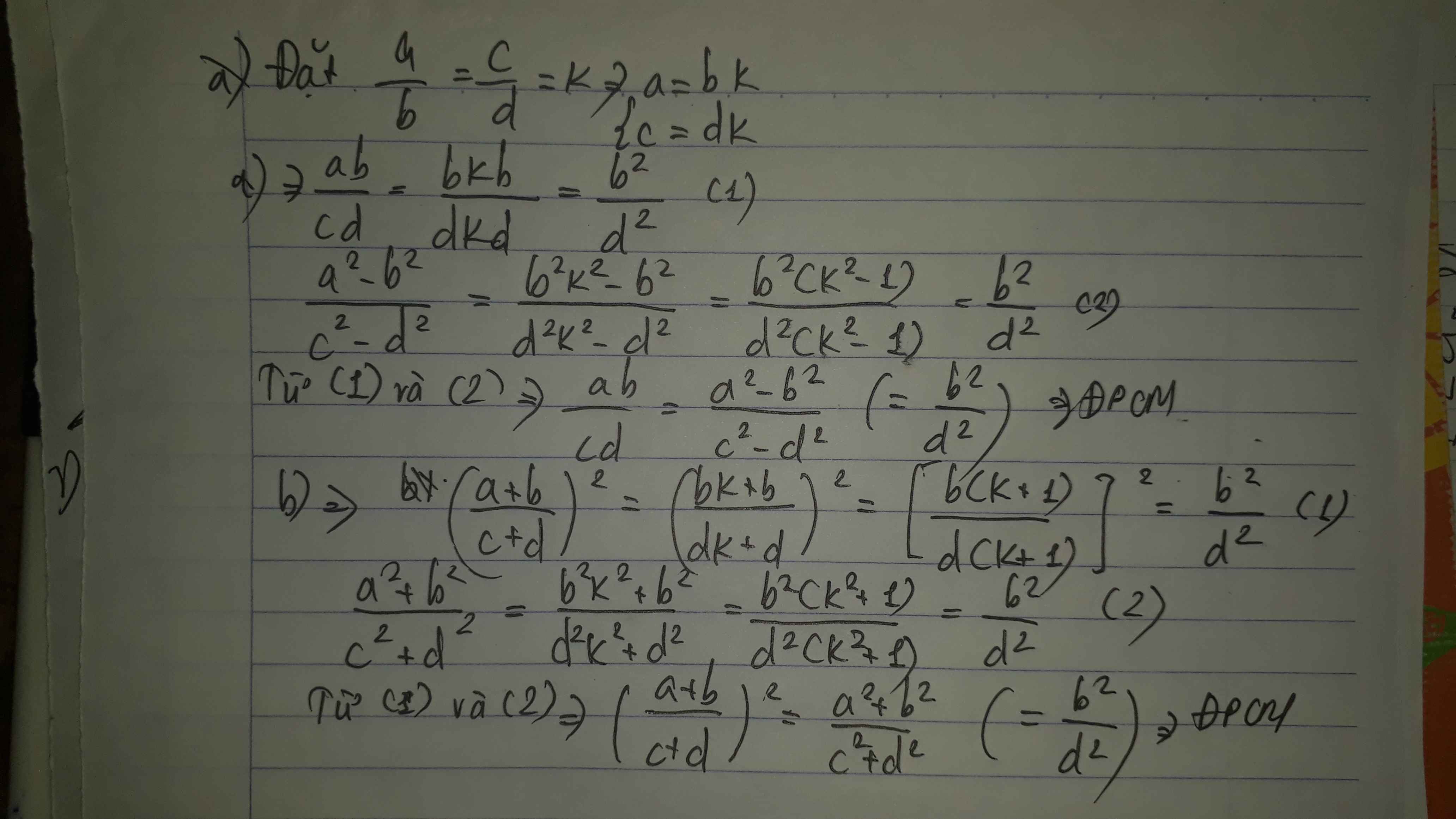
Bài 2:
Đặt a/b=c/d=k
=>a=bk; c=dk
a: \(\dfrac{a}{a+b}=\dfrac{bk}{bk+b}=\dfrac{k}{k+1}\)
\(\dfrac{c}{c+d}=\dfrac{dk}{dk+d}=\dfrac{k}{k+1}\)
Do đó: \(\dfrac{a}{a+b}=\dfrac{c}{c+d}\)
b: \(\dfrac{7a^2+5ac}{7a^2-5ac}=\dfrac{7\cdot b^2k^2+5\cdot bk\cdot dk}{7\cdot b^2k^2-5\cdot bk\cdot dk}\)
\(=\dfrac{7b^2k^2+5bdk^2}{7b^2k^2-5bdk^2}=\dfrac{7b^2+5bd}{7b^2-5bd}\)(đpcm)