Cho tam giác ABC, có góc B+ góc C= 60 độ, phân giác AD. Trên AD lấy điểm O. Trên tia đối của tia AC lấy điểm M sao cho góc ABM= góc ABO. Trên tia đối của AB lấy điểm N sao cho góc ACN= góc ACO. CMR:
a, AM=AN
b, Tam giác MON đều
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CH
Cô Hoàng Huyền
Admin
VIP
1 tháng 3 2018
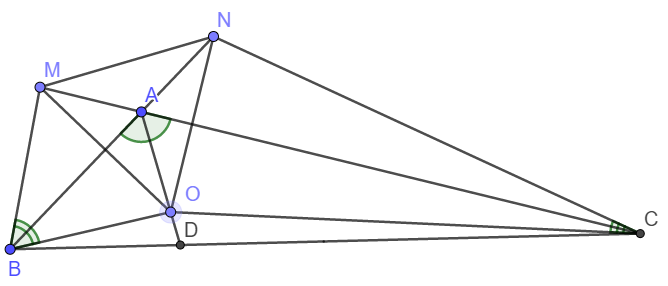
a) Xét tam giác ABC có \(\widehat{B}+\widehat{C}=60^o\Rightarrow BAC=120^o\)
Do AD là phân giác nên \(\widehat{BAD}=\widehat{CAD}=60^o\)
\(\widehat{MAB}\) và \(\widehat{BAC}\) là hai góc kề bù nên \(\widehat{MAB}=180^o-120^o=60^o\)
Vậy thì \(\Delta MAB=\Delta OAB\left(g-c-g\right)\)
\(\Rightarrow AM=AO\)
Hoàn toàn tương tự ta có AN = AO
Vậy nên AM = AN.
b) Ta có do \(\Delta MAB=\Delta OAB\Rightarrow AM=AO;BM=BO\)
Suy ra AB là trung trực của MO,.
Lại có N thuộc AB nên NM = NO
Hoàn toàn tương tự ta có MO = MN
Vậy OM = ON = MN hay OMN là tam giác đều.
CH
Cô Hoàng Huyền
Admin
VIP
1 tháng 3 2018
Em tham khảo tại link dưới đây nhé.
Câu hỏi của Nguyễn Hoàng Giang - Toán lớp 7 - Học toán với OnlineMath
HN
6 tháng 7 2017
Ta dễ dàng tính được ngay MABˆMAB^=BAOˆBAO^(dựa vào tia phân giác của góc BAC và góc ngoài của góc đó)
Xét tam giác ABM và tam giác ABO có:
BA là cạnh chung
MABˆMAB^=BAOˆBAO^
MBAˆMBA^=ABOˆABO^(gt)
=>tam giác ABM=tam giác ABO(g.c.g)
=>AM=AO.
Ta cũng dễ dàng tính được OACˆOAC^=CANˆCAN^(dựa vào tia phân giác của góc BAC và góc ngoài của góc đó)
Xét tam giác COA và tam giác CNA có:
AC là cạnh chung
OACˆOAC^=CANˆCAN^(c/m trên)
OACˆOAC^=ACNˆACN^(gt)
=>Tam giác COA=tam giác CNA(g.c.g)
=>AO=AN
Từ trên =>AN=AM
b)Ta Sẽ tính từ các kết luận trên được BN là trung trực của MO=>MN=NO
Tương tự trên cũng c/m được MC là trung trực của ON=>MO=MN
=>MN=MO=NO
=>Tam giác MON là tam giác đều.
7 tháng 7 2017
a) Xét tam giác ABC có \(\widehat{B}+\widehat{C}=60^o\)nên \(\widehat{A}=120^o\)
Do AD là tia phân giác nên \(\widehat{A}_1=\widehat{A_2}=\widehat{A}_3=\widehat{A}_4=60^o\)
tam giác ABM = tam giác ABO ( g.c.g )
suy ra AM = AO
tam giác ACN = tam giác ACO ( g.c.g )
suy ra AN = AO
suy ra AM = AN
b) tam giác AOM = tam giác AON ( c.g.c ) \(\Rightarrow\)OM = ON ( 1 )
tam giác AOM = tam giác ANM ( c.g.c ) \(\Rightarrow\)OM = MN ( 2 )
Từ ( 1 ) và ( 2 ) suy ra : OM = ON = MN
do đó tam giác MON đều
CH
Cô Hoàng Huyền
Admin
VIP
1 tháng 3 2018
Em tham khảo tại link dưới đây nhé.
Câu hỏi của Nguyễn Hoàng Giang - Toán lớp 7 - Học toán với OnlineMath
a) Xét tam giác ABC có ˆB+ˆC=60o⇒BAC=120oB^+C^=60o⇒BAC=120o
Do AD là phân giác nên ˆBAD=ˆCAD=60oBAD^=CAD^=60o
ˆMABMAB^ và ˆBACBAC^ là hai góc kề bù nên ˆMAB=180o−120o=60oMAB^=180o−120o=60o
Vậy thì ΔMAB=ΔOAB(g−c−g)ΔMAB=ΔOAB(g−c−g)
⇒AM=AO⇒AM=AO
Hoàn toàn tương tự ta có AN = AO
Vậy nên AM = AN.
b) Ta có do ΔMAB=ΔOAB⇒AM=AO;BM=BOΔMAB=ΔOAB⇒AM=AO;BM=BO
Suy ra AB là trung trực của MO,.
Lại có N thuộc AB nên NM = NO
Hoàn toàn tương tự ta có MO = MN
Vậy OM = ON = MN hay OMN là tam giác đều.
➩góc BAC =120 độ
ta có AD là phân giác
góc BAC=>BAD=CAD=\(\dfrac{1}{2}\)BAC=60 độ
△ABO và ΔABM có góc BAO= BAM=60 độ
AB chung
góc ABM =ABO
➩tam giác ABO =tam giác ABM (g.c.g)
➝AM=AO (*)
Ta chứng minh tương tự như trên:
tam giác ACO= tam giác ACN (g.c.g)
➝AN=AO(**)
Từ (*)(**) ⇒AM=AN (đpcm)