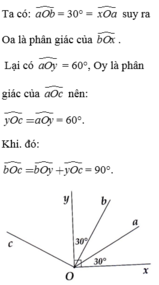
Cho hai tia Ox, Oy vuông góc với nhau. Trong góc xOy ta vẽ hai tia OA, OB sao cho AOx BOy 30o. Vẽ tia OC sao cho tia Oy là tia phân giác của góc AOC. Chứng tỏ rằng a. Tia OA là tia phân giác của góc BOxb. OB vuông góc với OC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 7 2016
a/
Ta có : Góc AOB = Góc xOy - góc AOx - góc bOy = 90o - 30o - 30o =30 o
=> Góc AOB = Góc AOx = 30 o
=> Tia OA là tia phân giác của góc BOx
Vậy tia OA là tia phân giác của góc BOx
b/ Do Oy là phân giác của góc AOC mà góc AOC = Góc AOB + góc BOy = 60o
=> Góc COy = Góc AOC=60o
Góc AON = Góc MON - góc AOM =120o - 90o =30o
Góc BON = Góc MON - Góc BON=120o - 90o =30o
=> Góc AON= Góc BOM
Góc xOy = Góc MON - Góc NOx -Góc MOy = Góc MON - góc AON/2- góc BOM/2 = 120o -30o/2 -30o/2 =90o
=> Ox vuông góc với Oy.
=> Góc BOC = Góc BOy + Góc BON = 60o + 30o =90o
=> OB vuông góc với tia OC.
CM
14 tháng 7 2018
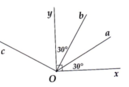
Ta có: a O b ^ = 30°= x O a ^ suy ra
Oa là phân giác của b O x ^ .
Lại có a O y ^ = 60°, Oy là phân
giác của a O c ^ nên:
y O c ^ = a O y ^ = 60°.
Khi. đó:
b O c ^ = b O y ^ + y O c ^ = 90°.
28 tháng 9 2021
góc xOB=90o-góc BOy
góc BOx=900-300=600
góc AOB=góc BOx-góc AOx
góc AOB = 60o-30o=30o
mà góc AOB=góc AOx=300
=> OA là phân giác của góc BOx
13 tháng 6 2021
Giải:
a) Vì Ox và Oy vuông góc với nhau
\(\Rightarrow x\widehat{O}y=90^o\)
\(\Rightarrow x\widehat{O}a+a\widehat{O}b+b\widehat{O}y=x\widehat{O}y\)
\(30^o+a\widehat{O}b+30^o=90^o\)
\(a\widehat{O}b=90^o-30^o-30^o\)
\(a\widehat{O}b=30^o\)
\(\Rightarrow x\widehat{O}a+a\widehat{O}b=x\widehat{O}b\)
\(30^o+30^o=x\widehat{O}b\)
\(\Rightarrow x\widehat{O}b=60^o\)
Vì +) \(x\widehat{O}a+a\widehat{O}b=x\widehat{O}b\)
+) \(x\widehat{O}a=a\widehat{O}b=30^o\)
⇒Oa là tia p/g của \(x\widehat{O}b\)
23 tháng 10 2015
a) Ta có : góc BOA = 900 - yOB - AOx
=) BOA = 900 - 300
=) BOA = 300
vì BOA = AOx = 300
=) OA là tia phân giác của góc BOx
b) Ta có : AOy = 900 - 300 = 600
Vì Oy là tia phân giác của Góc COA
=) Coy = yOA = 600
Vì COy là tia phân giác của góc COA
19 tháng 8 2017
a. Ta có: \(\widehat{AOB}+\widehat{AOx}+\widehat{BOy}=90^o\)
\(\Rightarrow\widehat{AOB}=90^o-\widehat{AOx}-\widehat{BOy}=90^o-30^o-30^o=30^o\)
\(\Rightarrow\widehat{AOB}=\widehat{AOx}=30^o\)
\(\Rightarrow\) OA là tia phân giác của \(\widehat{BOx}\)
b. Ta có: \(\widehat{AOy}=\widehat{AOB}+\widehat{BOy}=30^o+30^o=60^o\)
Vì Oy là tia phân giác của \(\widehat{AOC}\) nên:
\(\widehat{COy}=\widehat{AOy}=60^o\)
\(\Rightarrow\widehat{BOC}=\widehat{BOy}+\widehat{COy}=30^o+60^o=90^o\)
\(\Rightarrow OB\perp OC\)