Cho tam gaics ABC góc B=50 độ góc C= 30 độ, BC = 10cm .tính diện tích abc
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
0
:>>>>>>>>>
17 tháng 8 2023
3:
góc C=90-50=40 độ
Xét ΔABC vuông tại A có sin C=AB/BC
=>4/BC=sin40
=>\(BC\simeq6,22\left(cm\right)\)
\(AC=\sqrt{BC^2-AB^2}\simeq4,76\left(cm\right)\)
1:
góc C=90-60=30 độ
Xét ΔABC vuông tại A có
sin B=AC/BC
=>3/BC=sin60
=>\(BC=\dfrac{3}{sin60}=2\sqrt{3}\left(cm\right)\)
=>\(AB=\dfrac{2\sqrt{3}}{2}=\sqrt{3}\left(cm\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 8 2021
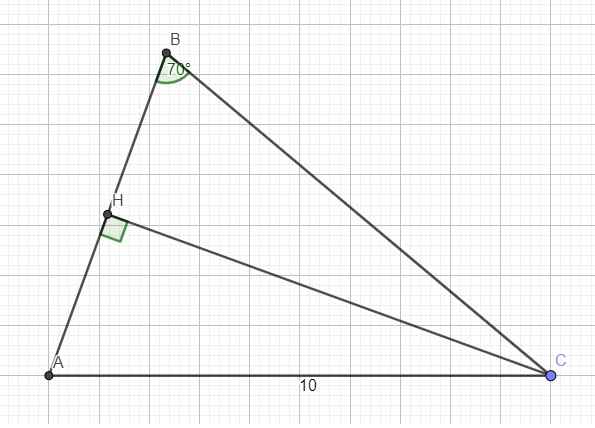
\(A=180^0-\left(B+C\right)=70^0\)
\(\Rightarrow A=B\Rightarrow\Delta ABC\) cân tại C
\(\Rightarrow BC=AC=10\left(cm\right)\)
Kẻ đường cao CH \(\Rightarrow\) H đồng thời là trung điểm AB
Trong tam giác vuông ACH:
\(cosA=\dfrac{AH}{AC}\Rightarrow AH=AC.cosA=10.cos70^0\approx3,42\left(cm\right)\)
\(AB=2AH\approx6,84\left(cm\right)\)
b. Cũng trong tam giác vuông ACH:
\(sinA=\dfrac{CH}{AC}\Rightarrow CH=AC.sinA=10.sin70^0\approx9,4\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}CH.AB\approx32,15\left(cm^2\right)\)
CP
16 tháng 7 2021
Ta có: HB + HC = BC
=>HC = 60 - HB (cm)
Xét △AHC vuông tại H có: \(tan\widehat{C}=\dfrac{AH}{HC}\Rightarrow tan30^0=\dfrac{AH}{HC}\Rightarrow HC=\dfrac{AH}{tan30^0}\left(cm\right)\) (1)
Xét △AHB vuông tại H có: \(tan\widehat{B}=\dfrac{AH}{HB}\Rightarrow tan20^0=\dfrac{AH}{60-HC}\Rightarrow tan20^0\left(60-HC\right)=AH\) (2)
Thay (1) vào (2) ta được: \(\Rightarrow tan20^0\left(60-\dfrac{AH}{tan30^0}\right)=AH \)
\(\Rightarrow tan20^0\left(\dfrac{60.tan30^0}{tan30^0}-\dfrac{AH}{tan30^0}\right)=AH\)
\(\Rightarrow tan20^0\left(\dfrac{60.tan30^0-AH}{tan30^0}\right)=AH\)
\(\Rightarrow tan20^0\left(60.tan30^0-AH\right)=AH.tan30^0\)
\(\Rightarrow tan20^0\left(20\sqrt{3}-AH\right)=AH.tan30^0\)
\(\Rightarrow tan20^0.20\sqrt{3}-AH.tan20^0=AH.tan30^0\)
\(\Rightarrow tan20^0.20\sqrt{3}=AH.\left(tan30^0+tan20^0\right)\)
\(\Rightarrow AH=\dfrac{tan20^0.20\sqrt{3}}{tan30^0+tan20^0}\approx13,3943\left(cm\right)\)
Diện tích của △ABC là: \(S_{ABC}=\dfrac{AH.BC}{2}=\dfrac{13,3943.60}{2}\approx401,83\left(cm^2\right)\)
Vậy...........
MN
1
Lời giải:
Từ $A$ kẻ $AH\perp BC$.
Xét tam giác $ABH$: $\frac{AH}{BH}=\tan B$
$\Rightarrow BH=\frac{AH}{\tan B}=\frac{AH}{\tan 50^0}$
Xét tam giác $ACH$: $\frac{AH}{CH}=\tan C$
$\Rightarrow CH=\frac{AH}{\tan C}=\frac{AH}{\tan 30^0}$
Do đó:
$BC=BH+CH=AH(\frac{1}{\tan 50^0}+\frac{1}{\tan 30^0})$
$10=AH(\frac{1}{\tan 50^0}+\frac{1}{\tan 30^0})$
$AH=3,89$ (cm)
$S_{ABC}=\frac{AH.BC}{2}=\frac{3,89.10}{2}=19,45$ (cm vuông)
Hình vẽ:
