Tất cả giá trị của tham số mm để đồ thị hàm số (C):\(y=-2x^3+3x^2+2m-1\) cắt trục hoành tại ba điểm phân biệt là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Phương trình hoành độ giao điểm là: m x 3 - x 2 2 x + 8 m = 0
⇔ m x + 2 x 2 - 2 x + 4 - x x + 2 = 0 ⇔ x + 2 m x 2 - 2 m x + 4 m - x = 0 ⇔ [ x = - 2 g x = m x 2 - 1 + 2 m x + 4 m = 0
Để đồ thị C m cắt trục hoành tại ba điểm phân biệt thì g x = 0 có 2 nghiệm phân biệt khác -2 ⇔ m ≠ 0 ∆ = 1 + 2 m 2 - 16 m 2 > 0 g - 2 = 4 m + 2 1 + 2 m + 4 m ≠ 0 ⇔ m ∈ - 1 6 ; 1 2 \ 0

Chọn B.
Phương trình hoành độ giao điểm:
![]()
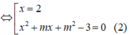
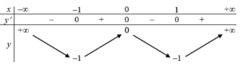
Để đồ thị hàm số đã cho cắt trục hoành tại ba điểm phân biệt ⇔ Phương trình (1) có ba nghiệm phân biệt ⇔ Phương trình (2) có hai nghiệm phân biệt khác 2
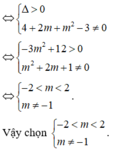

Đáp án B
Phương trình hoành độ giao điểm là
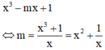
(Do x = 0 không phải là nghiệm của PT)
Xét hàm số
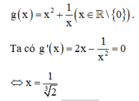
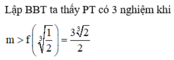

Chọn B.
Phương trình hoành độ giao điểm: -x4 + 2x2 + m = 0 ⇔ m = x4 - 2x2.
Đặt (C): y = x4 - 2x2 và d: y = m
Xét hàm số y = x4 - 2x2.
Ta có y' = 4x3 - 4x; y' = 0 ⇔ x = 0 ∨ x = -1 ∨ x = 1.
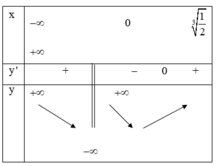
Bảng biến thiên:
Đồ thị hàm số đã cho cắt trục hoành tại ít nhất ba điểm phân biệt khi -1 < m < 0.
Vậy chọn -1 < m < 0a

Đáp án B
Phương pháp:
+) Xác định m để phương trình hoành độ giao điểm có 3 nghiệm phân biệt.
+) Cô lập m, sử dụng phương pháp hàm số.
Cách giải:
Phương trình hoành độ giao điểm của đồ thị hàm số y = x3 - mx + 1 và trục hoành là: x3 - mx + 1 = 0
⇔ x3 - mx + 1 = 0 ⇔ mx = x3 + 1(*)
+) x = 0:(*) ⇔ m.0 = 1: vô lý Phương trình (*) không có nghiệm x = 0 với mọi m
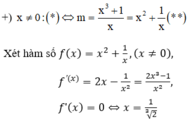
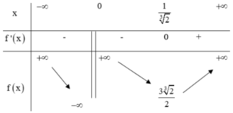
Số nghiệm của phương trình (**) là số giao điểm của đồ thị hàm số ![]() và đường thẳng y = m song song với trục hoành.
và đường thẳng y = m song song với trục hoành.
Để phương trình ban đầu có 3 nghiệm phân biệt ⇔ (**) có 3 nghiệm phân biệt khác 0
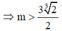
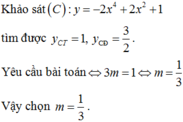



\(\Leftrightarrow2x^3-3x^2+1=2m\)
Xét hàm \(f\left(x\right)=2x^3-3x^2+1\)
\(f'\left(x\right)=6x^2-6x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
\(f\left(0\right)=1\) ; \(f\left(1\right)=0\)
\(\Rightarrow\) pt đã cho có 3 nghiệm pb (cắt trục hoành tại 3 điểm pb) khi và chỉ khi:
\(0< 2m< 1\Leftrightarrow0< m< \dfrac{1}{2}\)