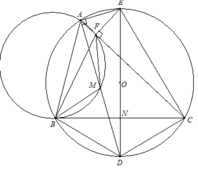
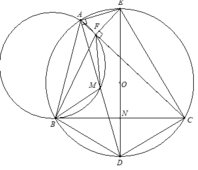
1/ Giả sử O là tâm đường tròn ngoại tiếp tam giác ABC, D là trung điểm cạnh AB, E là trọng tâm tam giác ACD. Chứng minh rằng nếu AB=AC thì OE vuông góc với CD.
2/Tam giác ABC và tam giác DEF cùng nội tiếp trong một đường tròn. Chứng minh rằng chu vi của chúng bằng nhau khi và chỉ khi có: sinA+sinB+sinC=sinD+sinE+sinF
3/Một đường thẳng chia một tam giác thành hai phần có diện tích bằng nhau và chu vi bằng nhau. Chứng minh rằng tâm đường tròn nội tiếp tam giác nằm trên đường thẳng ấy