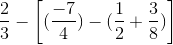
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(\frac{1}{2}xy-1\right).\left(x^3-2x-6\right)=\frac{1}{2}xy.\left(x^3-2x-6\right)+\left(-1\right).\left(x^3-2x-6\right)\)
= \(\frac{1}{2}xy.x^3+\frac{1}{2}xy.\left(-2x\right)+\frac{1}{2xy}.\left(-6\right)+\left(-1\right).x^3+\left(-1\right).\left(-2x\right)+\left(-1\right).\left(-6\right)\)
= \(\frac{1}{2}x^{\left(1+3\right)}y-x^{\left(1+1\right)}y-3xy-x^3+2x+6\)
= \(\frac{1}{2}x^4y-x^2y-3xy-x^3+2x+6\)
= \(\frac{1}{2}x^4y-x^3-x^2y-3xy+2x+6\)
Chúc bạn học tốt !!!
Bài làm
Ta có: ( xy - 1 )( x3 - 2x - 6 )
= ( xy . x3 ) + [ xy . ( -2x ) ] + [ xy . ( - 6 ) ] + [ ( -1 ) . x3 ] + [ ( -1 ) . ( -2x ) ] + [ ( -1 ) . ( -6 ) ] ( * chỗ này nếu thầnh thạo phép nnhân đa thức r thì k cần pk ghi đâu )
= x4y - 2x2y - 6xy - x3 + 2x + 6
# Học tốt #


Sử dụng tính chất : nếu a , b , c \(\in\) Z và a < b thì a + c < b - c . Từ đó
=> \(\frac{a}{m}< \frac{a+b}{2m}\) ( chia 2 vế cho m > 0 )
Vậy x < z ( 1 )
- Ta chứng minh z < y hay \(\frac{a+b}{2m}< \frac{b}{m}\)
Ta có : am < bm => am + bm < bm + bm ( cộng hai vế với bm )
=> ( a + b )m < 2bm
=> a + b < 2b ( chia 2 vế cho m )
=> \(\frac{a+b}{2m}< \frac{2b}{2m}=\frac{b}{m}\) ( chia 2 vế cho 2m )
Hay z < y ( 2 )
Từ ( 1 ) và ( 2 ) => x < z < y
* Nhận xét : từ kết quả trên ta rút ra kết luận : trên trục số , giữa 2 điểm hữu tỉ khác nhau bất kì bao giờ cũng có ít nhất một điểm hữu tỉ nữa và do đó có vô số điểm hữu tỉ . Ta bảo tập hợp Q là tập trù mật.


Cái bài này mình đã từng đăng để hỏi mấy bạn kia.
Nhưng đề câu này thiểu bạn ơi.
Phải có x=a/m ; y=b/m
À thôi, mk viết đầy đủ đề thử nhé !
Giả sử:x=a/m;y=b/m (a,b,m thuộc Z.m > 0) và x < y.
Hãy chứng minh (chứng tỏ) rằng nếu chọn z=a+b/2m thì ta có x < y < z.
Trong sách lớp 7 đề y như z đó !
Mk ghi cách làm luôn nha !
Giả sử x=a/m,y=b/m (a,b,m thuộc Z,m > 0 )
Vì x < y nên ta suy ra a < b.
ta có: x=a/m, y=b/m <=> x=2a/am. y=2b/2m
mà a < b nên a+a < a+b <=> 2a < a+b
Do 2a < a+b thì x < y ( 1 )
Ta lại có: a < b nên a+b < b+b <=> a+b < 2b
Mà a+b < 2b <=> x < z ( 2 )
Từ ( 1 ) và ( 2 ) suy ra x < y < z (ĐPCM)

 xy – 1 với đa thức x3 – 2x – 6.
xy – 1 với đa thức x3 – 2x – 6. (a, b, m ∈ Z; m > 0) và x < y. Hãy chứng minh nếu chọn
(a, b, m ∈ Z; m > 0) và x < y. Hãy chứng minh nếu chọn 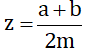 thì ta có x < z < y.
thì ta có x < z < y.
d) \(\dfrac{2}{3}-\left[\left(\dfrac{-7}{4}\right)-\left(\dfrac{1}{2}+\dfrac{3}{8}\right)\right]\)
\(=\dfrac{2}{3}-\left[\left(\dfrac{-7}{4}\right)-\left(\dfrac{4}{8}+\dfrac{3}{8}\right)\right]\)
\(=\dfrac{2}{3}-\left[\left(\dfrac{-14}{8}-\dfrac{7}{8}\right)\right]=\dfrac{2}{3}-\left(\dfrac{-21}{8}\right)\)
\(=\dfrac{16}{24}+\dfrac{63}{24}=\dfrac{79}{24}\)
Hok tốt