Cho tam giác ABC vuông tại A. Đường tròn nội tiếp tam giác ABC tiếp xúc với BC tại D. Chứng minh rằng :
\(S_{ABC}=BD.DC\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
Nguyen Thuy Hoa
24 tháng 6 2017
Đúng(1)
Những câu hỏi liên quan
CM
26 tháng 8 2017
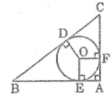
Gọi E và F lần lượt là tiếp điểm của đường tròn với AD và AC
Theo tính chất hai tiếp tuyến cắt nhau, ta có:
AE = AF
BE = BD
CD = CF
BD = BC + CD
BE = AB – AE
Suy ra: BD + BE = AB + BC – (AE + CD)
= AB + BC – (AE + CE)
= AB + BC – AC
Suy ra: BD = (AB + BC - AC)/2
Lại có: CD = BC – BD
CF = AC = AF
Suy ra: CD + CF = BC + AC – (BD + AF)
= BC + AC – (BE + AE)
= BC + AC – BA
Vậy S A B C = BD.DC.
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 1 2022
Pitago: \(BC^2=AB^2+AC^2\Rightarrow BC^2-\left(AB^2+AC^2\right)=0\)
Gọi các tiếp điểm với AB và AC là E và F
Do đường tròn (I) nội tiếp tam giác, theo t/c hai tiếp tuyến cắt nhau:
\(BD=BE\) ; \(AE=AF\) ; \(CD=CF\)
Mà \(BD+CD=BC;AE+BE=AB;AF+CF=AC\)
\(\Rightarrow BC+AB-AC=BD+CD+AB+BE-AF-CF=BD+BE=2BD\)
\(\Rightarrow BD=\dfrac{BC+AB-AC}{2}\)
Tương tự: \(BC+AC-AB=2DC\Rightarrow DC=\dfrac{BC+AC-AB}{2}\)
\(\Rightarrow BD.DC=\dfrac{1}{4}\left(BC+AB-AC\right)\left(BC+AC-AB\right)=\dfrac{1}{4}\left[BC^2-\left(AB-AC\right)^2\right]\)
\(=\dfrac{1}{4}\left(BC^2-\left(AB^2+AC^2\right)+2AB.AC\right)=\dfrac{1}{2}AB.AC=S_{ABC}\)
HH
19 tháng 7 2020
Đặt BC = a , AC = b , AB = c . Ta có :
\(BD=\frac{a+c-d}{2}\)
\(DC=\frac{a+b-c}{2}\)
Do đó , ta giả sử \(\left(b\ge c\right)\)
\(BD.DC=\frac{a+c-b}{2}.\frac{a+b-c}{2}\)
\(=\frac{a-\left(b-c\right)}{2}.\frac{a+\left(b-c\right)}{2}\)
\(=\frac{a^2-\left(b-c\right)^2}{4}\)
\(=\frac{a^2-b^2+2bc-c^2}{4}\)
\(=\frac{a^2-\left(b^2+c^2\right)+2bc}{4}\)
Do \(a^2=b^2+c^2\)nên \(BD.DC=\frac{2bc}{3}=\frac{bc}{2}=S_{ABC}\)
Q
13 tháng 11 2016
Gọi E, F lần lượt là tiếp điểm của đường tròn đã cho với các cạnh AB, AC. Đặt AE = AF = x. Ta có BD = BE, CF = CD. Từ đó ta có:
AB.AC = ( x + BD )( x + CD ) = x2 + ( BD + DC )x + BD.CD (1)
Do ABC là tam giác vuông nên theo định lý Pytago, ta có:
AB2 + AC2 = BC2 trở thành ( x + BD )2 + ( x + CD )2 = ( DB + DC )2 <=> ( x2 + ( BD + DC )x) = BD.DC <=> ( x + BD )( x + CD ) = 2BD.CD (2).
Từ (1), (2) suy ra đpcm.
HD
25 tháng 1 2017
cho 1 hinh duoc tao bang nua hinh tron co duong tron 2 dm va 1 hinh tam giac co duong cao 3dm,day2dm
lam on hay giup minh nhe! co giao minh sap kiem tra rui. cam on
LN
Lưu Nguyễn Hà An
CTVHS
13 tháng 8 2023
THAM KHẢO NHÉ. XIN LỖI VÌ KO TRÙNG ĐỀ
Giải thích các bước giải:
a.Gọi là tâm đường tròn bàng tiếp trong góc
lần lượt là phân giác ngoài tại đỉnh
Ta có tiếp xúc lần lượt tại
là tiếp tuyến của
b.Vì tiếp xúc với tại là tiếp tuyến của
Ta có là tiếp tuyến của
là tiếp tuyến của
c.Ta có: