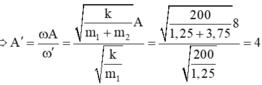Phần tải trọng đặt trên các lò xo của một xe LIMOUSINE có khối lượng
là m1 = 1000 (kg). Khi xe chở số hành khách với khối lượng tổng cộng là m2 =
325 (kg) và chuyển động đều trên đoạn đường xấu có những rãnh cách nhau 4 (m)
thì xe bị xóc mạnh nhất, khi đó vận tốc của xe là v = 16 (km/h). Lấy g2 =9,8 (m/s
). Khi xe đến bến, mọi người rời khỏi xe thì phần tải trọng có khối lượng m1 nhô
lên cao một đoạn xấp xỉ là
A. 3,5 (cm). B. 5 (cm). C. 6,5 (cm). D. 8 (cm).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
+ Tốc độ của hệ hai vật khi đi qua vị trí cân bằng v = v k m 1 + m 2 1 200 1 , 25 + 3 , 75 max
Khi đi qua vị trí cân bằng vật m 1 (tốc độ của m 1 cực đại khi đi qua vị trí cân bằng và giảm dần khi đến biên) và chuyển động thằng đều bới vận tốc
+ Biên độ dao động mới của vật m 1 là A 2 = V max ω ' 16 π 200 1 , 25
+ Lò xo giãn cực đại lần đầu tiền khi m 1 đến biên, ứng với khoảng thời gian Δt = T 4 = 2 π 4 m 1 k = 1 8 s kể từ thời điểm hai vật tách khỏi nhau.
→ khoảng cách giữa hai vật Δx = v 2 1 8 max

Hướng dẫn:
Ta nhận thấy rằng, trong quá trình chuyển động đến một thời điểm nào đó vật m 2 sẽ tách khỏi vật m 1 , biến cố này chỉ làm thay đổi tần số dao động riêng của vật dao động điều hòa mà không làm thay đổi vị trí cân bằng của hệ dao động điều hòa.
Mặc khác, tại vị trí cân bằng hai vật sẽ có tốc độ cực đại, ngay sau đó vật m 1 sẽ chuyển động chậm dần về biên, vật m 2 thì chuyển động thẳng đều với vận tốc cực đại do đó hai vật sẽ tách ra khỏi nhau tại vị trí này.
Để đơn giản, ta có thể thay thế chuyển động của vật thành hai giai đoạn chuyển động thành phần.
Giai đoạn 1: Hai vật dao động điều hòa với biên độ A = 8 cm quanh vị trí cân bằng O từ biên về vị trí cân bằng.
+ Tần số góc dao động của hệ ω = k m 1 + m 2 = 200 1 , 25 + 3 , 75 = 2 π rad/s.
→ Khi hệ hai vật đến O, ta có v = v m a x = ω A = 2 π . 8 = 16 π c m / s .
Giai đoạn 1: Vật m1 dao động điều hòa quanh vị trí cân bằng O, vật m2 chuyển động thẳng đều ra xa với tốc độ v 2 = v m a x .
+ Tần số góc của con lắc sau khi vật m 2 tách ra khỏi m 1 ω ' = k m 1 = 200 1 , 25 = 4 π rad/s → T = 0,5 s.
Tại vị trí vật m 2 tách khỏi vật m 1 , ta có x′ = 0, v′ = vmax.
→ Biên độ dao động mới của m 1 là A 1 = v m a x ω ' = 16 π 4 π = 4 cm.
+ Lò xo giãn cực đại lần đầu tiên kể từ thời điểm hai vật tách nhau ứng với Δt = 0,25T = 0,125 s.
→ Khoảng cách giữa hai vật lúc đó là Δ x = x 2 – x 1 = v 2 Δ t – A 1 = 16 π . 0 , 125 – 4 = 2 π – 4 c m .
Đáp án A

Đáp án A
Ta có thể chia quá trình diễn ra của bài toán thành hao giai đoạn sau:
Giai đoạn 1: Hệ con lắc gồm lò xo có độ cứng k và vật m = m1+ m2 dao động điều hòa với biên độ A = 8 cm quanh vị trí cân bằng O vị trí lò xo không biến dạng.
+) Tần số góc của dao động 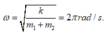
+) Tốc độ của hệ hai vật khi đi qua vị trí cân bằng ![]()
Giai đoạn 2: Vật m2 tách ra khỏi vật m1 tại O chuyển động thẳng đều với vận tốc vo, vật m1 vẫn dao động điều hòa quanh O.
+) Tần số góc của dao động m1: 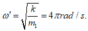
+) Biên độ dao động của m1: ![]()
Lò xo giãn cực đại lần đầu tiên ứng với m1 đang ở vị trí biên, khi đó m2 đã chuyển động với khoảng thời gian tương ứng là ![]()
Khoảng cách giữa hai vật: ![]()

Đáp án A
Tại vị trí cân bằng hai vật sẽ có tốc độ cực đại, ngay sau đó vật m 1 sẽ chuyển động chậm dần về biên, vật m2 thì chuyển động thẳng đều với vận tốc cực đại do đó hai vật sẽ tách ra khỏi nhau tại vị trí này
Lò xo giãn cực đại lần đầu tiên khi m 1 đi đến biên dương lần đầu, biên độ dao động của vật m 1 sau khi m 2 tác khỏi là
![]()
![]()
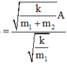
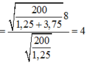
Chu kì dao động mới của m 1 :
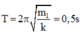
thời gian để vật đi từ vị trí cân bằng đến vị trí lò xo giãn cực đại (x = +A) lần đầu tiên là

Quãng đường mà m 2 đã đi được trong khoảng thời gian này
![]()
Khoảng cách giữa hai vật sẽ là
![]()
![]()