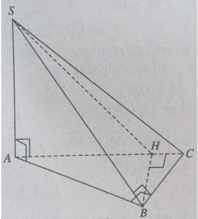
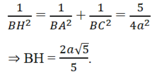Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, SA vuông góc với đáy
a) Chứng minh tam giác SBC vuông
b) Gọi H là chân đường cao vẽ từ B của tam giác ABC. Chứng minh \(\left(SAC\right)\perp\left(SBH\right)\)
c) Cho AB = a, BC = 2a. Tính khoảng cách từ B đến mặt phẳng (SAC)