Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
VT = a ( b + c ) − b ( a − c ) = ab + ac − ba + bc = ( ab − ab ) + ( ac + bc ) = 0 + a + b . c = VP Vậy a ( b + c ) − b ( a − c ) = ( a + b ) . c
VT = a ( b + c ) − b ( a − c ) = ab + ac − ba − bc = ab + ac − ba + bc = ac + bc = c ( a + b ) = VP ( dpcm )
a.(b+c)-b.(a-c)
=a.b+a.c-b.a+b.c
=(a.b-b.a)+a.b+b.c
=0+(a+b).c=(a+b).c(đpcm)
Ta có a .(b + c) - b .(a +c)
=a.b + a.c - b.a + b.c
=a.b - b.a + a.c + b.c
=0 + (a + b) . c
= (a +b) . c
\(a\left(b-c\right)-a\left(b+d\right)=-a\left(c+d\right)\)
\(\Leftrightarrow a[\left(b-c\right)-\left(b+d\right)]=-a\left(c+d\right)\)
\(\Leftrightarrow a\left(b-c-b-d\right)=-a\left(c+d\right)\)
\(\Leftrightarrow a\left(-c-d\right)=-a\left(c+d\right)\)
\(\Leftrightarrow-a\left(c+d\right)=-a\left(c+d\right)\)
vậy ...
KHAI TRIEN VE TRAI
(a+b)(c+d)-(a+d)(b+c)
=ac+ad+bc+bd-ab-ac-bd-cd
=ad+bc-ab-cd
=a(-b+d)-c(-b+d)
=(a-c)(-b+d) GIONG NHU VE PHAI
THAY DUNG THI
a(b-c)+c(a-b)=b(a-c)
ab - ac + ca - cb - ba + cb = 0
(ab - ab) - (bc - bc) - (ac - ac) =0
0 - 0 -0 = 0 (đpcm)
a, a(b+c)−b(a−c)a(b+c)−b(a−c)
=ab+ac−(ab−bc)=ab+ac−(ab−bc)
=ab+ac−ab+bc=ab+ac−ab+bc
=ac+bc=ac+bc
=(a+b)c=(a+b)c
b,(a+b)(a−b)(a+b)(a−b)
=(aa+ab)−(ab+bb)=(aa+ab)−(ab+bb)
=aa+ab−ab−bb
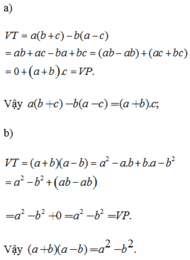
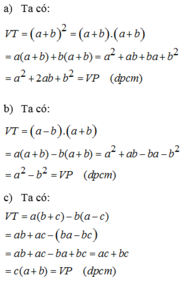
a, \(a\left(b+c\right)-b\left(a-c\right)\)
\(=ab+ac-\left(ab-bc\right)\)
\(=ab+ac-ab+bc\)
\(=ac+bc\)
\(=\left(a+b\right)c\)
b,\(\left(a+b\right)\left(a-b\right)\)
\(=\left(aa+ab\right)-\left(ab+bb\right)\)
\(=aa+ab-ab-bb\)
\(=aa-bb\)
\(=a^2-b^2\)