Cho tam giác ABC cân tại A, điểm D nằm giữa B và C. Chứng minh rằng độ dài AD nhỏ hơn cạnh bên của tam giác ABC ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 5 2019
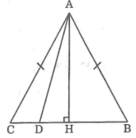
Kẻ AH ⊥ BC.
* Trường hợp H trùng với D
Ta có AH < AC (đường vuông góc ngắn hơn đường xiên)
Suy ra: AD < AC
* Trường hợp H không trùng với D
Giả sử D nằm giữa H và C.
Ta có: HD < HC
Suy ra: AD < AC (hình chiếu nhỏ hơn thì có đường xiên nhỏ hơn)
Vậy AD nhỏ hơn cạnh bên của tam giác cân ABC.
23 tháng 3 2017
Xét tgABD và tgACD có: AB=AC(GT) BD=DC vì D là trung điểm của BC và lại có AD chung=>tgABD=ACD(c.c.c)
góc ADB=ADC HAI GÓC TG UNG VÀ LẠI CÓ ADB+ACD=180o kề bù => ADB=ACD=900
Theo dinh ly pytago tổng binh p hai cah goc vuong bg bp canh huyền vay BD hay DC nho hon AB hay AC
9 tháng 3 2019
Bài 1 :
Vì tam giác đó cân
=>
- Có 2 cạnh là 4m
- Có 2 cạnh là 9m
Mà theo bất đẳng thức tam giác , độ dài 1 cạnh bao nhờ cũng nhỏ hơn tổng độ dài 2 cạnh còn lại
=> Tam giác đó có 2 cạnh bằng 9m .
Chu vi tam giác đó là :
9 + 9 + 4 = 22 ( m)
Đáp số : 22m
CM
19 tháng 9 2018
Trong ΔABD, ta có:
AD < AB + BD (bất đẳng thức tam giác) (1)
Trong ΔADC, ta có:
AD < AC + DC (bất đẳng thức tam giác) (2)
Cộng từng vế (1) và (2), ta có:
2AD < AB + BD + AC + DC ⇔ 2AD < AB + AC + BC
Vậy AD < (AB + AC + BC) / 2 .
19 tháng 9 2023
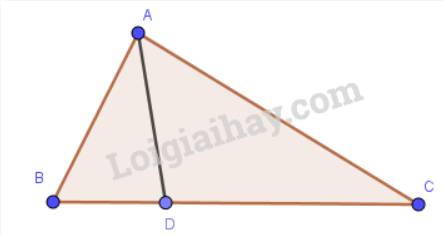
Áp dụng quan hệ giữa ba cạnh của tam giác ABD, ta có: AD < AB + BD
Áp dụng quan hệ giữa ba cạnh của tam giác ACD, ta có: AD < CD + AC
\(\Rightarrow AD + AD < AB+BD+CD+AC\)
\(\Rightarrow 2AD<AB+BC+AC\) ( vì \(DB+DC=BC\))
\(\Rightarrow\) 2AD < Chu vi tam giác ABC hay AD < (Chu vi tam giác ABC) : 2
Vậy AD nhỏ hơn nửa chu vi tam giác ABC.
18 tháng 5 2022
XétΔABD có AD<AB+BD(1)
Xét ΔACD có AD<AC+CD(2)
Từ (1) và (2) suy ra \(2AD< AB+AC+BC\)
hay \(AD< \dfrac{AB+AC+BC}{2}=\dfrac{C_{ABC}}{2}\)
28 tháng 4 2023
b: Xét ΔBAD và ΔBED có
BA=BE
góc ABD=góc EBD
BD chung
=>ΔBAD=ΔBED
=>góc BED=90 độ và DA=DE
c: DA=DE
DE<DC
=>DA<DC
8 tháng 4 2023
a: AE/BC=AE/AB=5,6/16=7/20
AD/AC=3,5/10=7/20
=>AE/AB=AD/AC
=>ΔAED đồg dạng với ΔABC
b: ΔAED đồng dạng với ΔABC
=>DE/BC=AE/AB
=>DE/16=7/20
=>DE=5,6cm
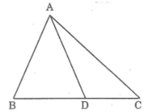
Kẻ \(AH\perp BC\)
- Nếu D trùng H thì \(AD< AC\) vì \(AH< AC\) ( đường vuông góc nhỏ hơn đường xiên )
- Nếu D không trùng H, giả sử D nằm giữa H và C. Ta có: \(HD< HC\)
\(\Rightarrow AD< AC\) ( hình chiếu nhỏ hơn thì đường xiên nhỏ hơn )
Vậy AD nhỏ hơn cạnh bên của \(\Delta ABC\)