Tìm \(x\in Q\), biết rằng :
a) \(\dfrac{11}{12}-\left(\dfrac{2}{5}+x\right)=\dfrac{2}{3}\)
b) \(2x\left(x-\dfrac{1}{7}\right)=0\)
c) \(\dfrac{3}{4}+\dfrac{1}{4}:x=\dfrac{2}{5}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 7 2017
a) \(\dfrac{11}{12}-\left(\dfrac{2}{5}+x\right)=\dfrac{2}{3}\)
\(\Leftrightarrow\dfrac{2}{5}+x=\dfrac{11}{12}-\dfrac{2}{3}\)
\(\Leftrightarrow\dfrac{2}{5}+x=\dfrac{1}{4}\)
\(\Leftrightarrow x=-\dfrac{3}{20}\in Q\) ( thỏa mãn )
Vậy x = \(-\dfrac{3}{20}\)
b) \(2x.\left(x-\dfrac{1}{7}\right)=0\)
\(\Leftrightarrow3x-2x.\dfrac{1}{7}=0\) (1)
mà \(x\in Q\) \(\Rightarrow2x.\dfrac{1}{7}\in Q\)(2)
Từ (1) và (2) \(\Rightarrow2x.\dfrac{1}{7}=0\)
\(\Rightarrow2x=\dfrac{1}{7}:0=0\)
\(\Rightarrow x=0:2=0\in Q\) (thỏa mãn)
Vậy x=0
c) \(\dfrac{3}{4}+\dfrac{1}{4}:x=\dfrac{2}{5}\)
\(\Leftrightarrow\dfrac{1}{4}:x=\dfrac{3}{4}-\dfrac{2}{5}\)
\(\Leftrightarrow\dfrac{1}{4}:x=\dfrac{7}{20}\)
\(\Leftrightarrow x=\dfrac{1}{4}:\dfrac{7}{20}\)
\(\Leftrightarrow x=\dfrac{5}{7}\in Q\)(thỏa mãn )
Vậy x= \(\dfrac{5}{7}\)
15 tháng 5 2022
a: (x+1/2)(2/3-2x)=0
=>x+1/2=0 hoặc 2/3-2x=0
=>x=-1/2 hoặc x=1/3
b: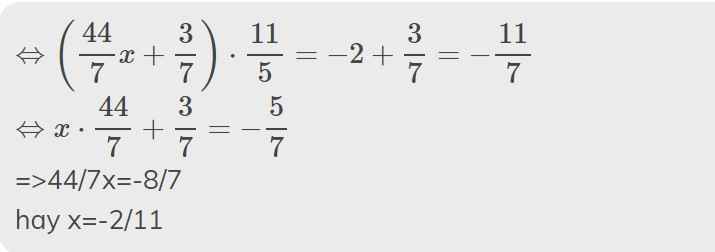 
c: \(\Leftrightarrow x\cdot\left(\dfrac{13}{4}-\dfrac{7}{6}\right)=\dfrac{5}{12}+\dfrac{5}{3}=\dfrac{5}{12}+\dfrac{20}{12}=\dfrac{25}{12}\)
\(\Leftrightarrow x=\dfrac{25}{12}:\dfrac{39-14}{12}=\dfrac{25}{25}=1\)
29 tháng 1 2022
a: =>1/2x=7/2-2/3=21/6-4/6=17/6
=>x=17/3
b: =>2/3:x=-7-1/3=-22/3
=>x=2/3:(-22/3)=-1/11
c: =>1/3x+2/5x-2/5=0
=>11/15x=2/5
hay x=6/11
d: =>2x-3=0 hoặc 6-2x=0
=>x=3/2 hoặc x=3
28 tháng 2 2022
a: =>x-3/4=1/6-1/2=1/6-3/6=-2/6=-1/3
=>x=-1/3+3/4=-4/12+9/12=5/12
b: =>x(1/2-5/6)=7/2
=>-1/3x=7/2
hay x=-21/2
c: (4-x)(3x+5)=0
=>4-x=0 hoặc 3x+5=0
=>x=4 hoặc x=-5/3
d: x/16=50/32
=>x/16=25/16
hay x=25
e: =>2x-3=-1/4-3/2=-1/4-6/4=-7/4
=>2x=-7/4+3=5/4
hay x=5/8
AT
20 tháng 6 2017
a/dễ --> tự lm
b/ \(\left(x-\dfrac{4}{7}\right)\left(1\dfrac{3}{5}+2x\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x-\dfrac{1}{5}=0\\1\dfrac{3}{5}+2x=0\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{5}\\2x=\dfrac{8}{5}\Rightarrow x=\dfrac{4}{5}\end{matrix}\right.\)
Vậy...............
c/ \(\left(x-\dfrac{4}{7}\right):\left(x+\dfrac{1}{2}\right)>0\)
TH1: \(\left\{{}\begin{matrix}x-\dfrac{4}{7}>0\\x+\dfrac{1}{2}>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x>\dfrac{4}{7}\\x>-\dfrac{1}{2}\end{matrix}\right.\) \(\Rightarrow x>\dfrac{4}{7}\)
TH2: \(\left\{{}\begin{matrix}x-\dfrac{4}{7}< 0\\x+\dfrac{1}{2}< 0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x< \dfrac{4}{7}\\x< -\dfrac{1}{2}\end{matrix}\right.\) \(\Rightarrow x< -\dfrac{1}{2}\)
Vậy \(x>\dfrac{4}{7}\) hoặc \(x< -\dfrac{1}{2}\) thì thỏa mãn đề
d/ \(\left(2x-3\right):\left(x+1\dfrac{3}{4}\right)< 0\)
TH1: \(\left\{{}\begin{matrix}2x-3>0\\x+1\dfrac{3}{4}< 0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x>1,5\\x< -\dfrac{7}{4}\end{matrix}\right.\)(vô lý)
TH2: \(\left\{{}\begin{matrix}2x-3< 0\\x+1\dfrac{3}{4}>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x< 1,5\\x>-\dfrac{7}{4}\end{matrix}\right.\)\(\Rightarrow-\dfrac{7}{4}< x< 1,5\)
Vậy...................
H9
HT.Phong (9A5)
CTVHS
1 tháng 11 2023
a) \(\dfrac{2}{3}x-\dfrac{1}{2}x=\left(-\dfrac{7}{12}\right)\cdot1\dfrac{2}{5}\)
\(\Rightarrow\dfrac{1}{6}x=\left(-\dfrac{7}{12}\right)\cdot\dfrac{7}{5}\)
\(\Rightarrow\dfrac{1}{6}x=-\dfrac{49}{60}\)
\(\Rightarrow x=-\dfrac{49}{60}:\dfrac{1}{6}\)
\(\Rightarrow x=-\dfrac{49}{10}\)
b) \(\left(\dfrac{1}{5}-\dfrac{3}{2}x\right)^2=\dfrac{9}{4}\)
\(\Rightarrow\left(\dfrac{1}{5}-\dfrac{3}{2}x\right)^2=\left(\pm\dfrac{3}{2}\right)^2\)
+) \(\dfrac{1}{5}-\dfrac{3}{2}x=\dfrac{3}{2}\)
\(\Rightarrow\dfrac{3}{2}x=\dfrac{1}{5}-\dfrac{3}{2}\)
\(\Rightarrow\dfrac{3}{2}x=-\dfrac{13}{10}\)
\(\Rightarrow x=-\dfrac{13}{10}:\dfrac{3}{2}\)
\(\Rightarrow x=-\dfrac{13}{15}\)
+) \(\left(1,25-\dfrac{4}{5}x\right)^3=-125\)
\(\Rightarrow\left(\dfrac{5}{4}-\dfrac{4}{5}x\right)^3=\left(-5\right)^3\)
\(\Rightarrow\dfrac{5}{4}-\dfrac{4}{5}x=-5\)
\(\Rightarrow\dfrac{4}{5}x=\dfrac{5}{4}+5\)
\(\Rightarrow\dfrac{4}{5}x=\dfrac{25}{4}\)
\(\Rightarrow x=\dfrac{25}{4}:\dfrac{4}{5}\)
\(\Rightarrow x=\dfrac{125}{16}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
1 tháng 11 2023
a, \(\dfrac{2}{3}\)\(x\) - \(\dfrac{1}{2}\)\(x\) = (- \(\dfrac{7}{12}\)). 1\(\dfrac{2}{5}\)
\(x\).(\(\dfrac{2}{3}\) - \(\dfrac{1}{2}\)) = (- \(\dfrac{7}{12}\)) . \(\dfrac{7}{5}\)
\(x\). \(\dfrac{1}{6}\) = - \(\dfrac{49}{60}\)
\(x\) = - \(\dfrac{49}{60}\).6
\(x\) = -\(\dfrac{49}{10}\)
TT
7 tháng 10 2017
a. \(\dfrac{11}{13}-\left(\dfrac{5}{42}-x\right)=-\left(\dfrac{15}{28}-\dfrac{11}{13}\right)\)
\(\Rightarrow\dfrac{11}{13}-\left(\dfrac{5}{42}-x\right)=-\left(\dfrac{-113}{364}\right)=\dfrac{113}{364}\)
\(\Rightarrow\left(\dfrac{5}{42}-x\right)=\dfrac{11}{13}-\dfrac{113}{364}\)
\(\Rightarrow\left(\dfrac{5}{42}-x\right)=\dfrac{15}{28}\)
\(\Rightarrow x=\dfrac{5}{42}-\dfrac{15}{28}=\dfrac{-5}{12}\)
Vậy..............
b. \(2x.\left(x-\dfrac{1}{7}\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}2x=0\\x-\dfrac{1}{7}=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{-1}{7}\end{matrix}\right.\)
Vậy............
c. \(\dfrac{3}{4}+\dfrac{1}{4}:x=\dfrac{2}{5}\)
\(\Rightarrow\dfrac{1}{4}:x=\dfrac{2}{5}-\dfrac{3}{4}\)
\(\Rightarrow\dfrac{1}{4}:x=\dfrac{-7}{20}\)
\(\Rightarrow x=\dfrac{1}{4}:\dfrac{-7}{20}=\dfrac{-5}{7}\)
Vậy...........
a)\(\dfrac{11}{12}-\left(\dfrac{2}{5}+x\right)=\dfrac{2}{3}\)
\(\dfrac{2}{5}+x=\dfrac{11}{12}-\dfrac{2}{3}\)
\(\dfrac{2}{5}+x=\dfrac{11}{12}-\dfrac{8}{12}\)
\(\dfrac{2}{5}+x=\dfrac{3}{12}\)
\(\dfrac{2}{5}+x=\dfrac{1}{4}\)
\(x=\dfrac{1}{4}-\dfrac{2}{5}\)
\(x=\dfrac{5}{20}-\dfrac{8}{20}\)
\(x=\dfrac{-3}{20}\)
b)\(2x\left(x-\dfrac{1}{7}\right)=0\)
\(\Rightarrow2x=0\) hoặc \(x-\dfrac{1}{7}=0\)
\(x=0:2\) \(x=0+\dfrac{1}{7}\)
\(x=0\) \(x=\dfrac{1}{7}\)
\(\Rightarrow x=0\) hoặc \(x=\dfrac{1}{7}\)
c)\(\dfrac{3}{4}+\dfrac{1}{4}:x=\dfrac{2}{5}\)
\(\dfrac{1}{4}:x=\dfrac{2}{5}-\dfrac{3}{4}\)
\(\dfrac{1}{4}:x=\dfrac{8}{20}-\dfrac{15}{20}\)
\(\dfrac{1}{4}:x=\dfrac{-7}{20}\)
\(x=\dfrac{1}{4}:\dfrac{-7}{20}\)
\(x=\dfrac{1}{4}.\dfrac{-20}{7}\)
x= \(\dfrac{1.\left(-5\right)}{1.7}\)
\(x=\dfrac{-5}{7}\)