Tìm giá trị của \(a\) và \(b\) để hai đường thẳng \(\left(d_1\right):\left(3a-1\right)x+2by=56\) và \(\left(d_2\right):\dfrac{1}{2}ax-\left(3b+2\right)y=3\) cắt nhau tại điểm \(M\left(2;-5\right)\).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
31 tháng 12 2021
b: Để hai đường thẳng cắt nhau tại một điểm trên trục tung thì m-1=15
hay m=16
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 11 2021
Tình cờ hay cố ý mà dữ liệu bài toán có rất nhiều sự trùng hợp dẫn đến lời giải rất dễ dàng:
\(M\in d_1\Rightarrow y_M=\left(m^2+1\right)x_M-2\Rightarrow y_M+2=\left(m^2+1\right)x_M\)
\(\Rightarrow A=2020\left(m^2+1\right)x_M^2\ge0\)
\(A_{min}=0\) khi \(m=0\)
Khi đó điểm M là \(M\left(0;-2\right)\)
29 tháng 8 2023
a: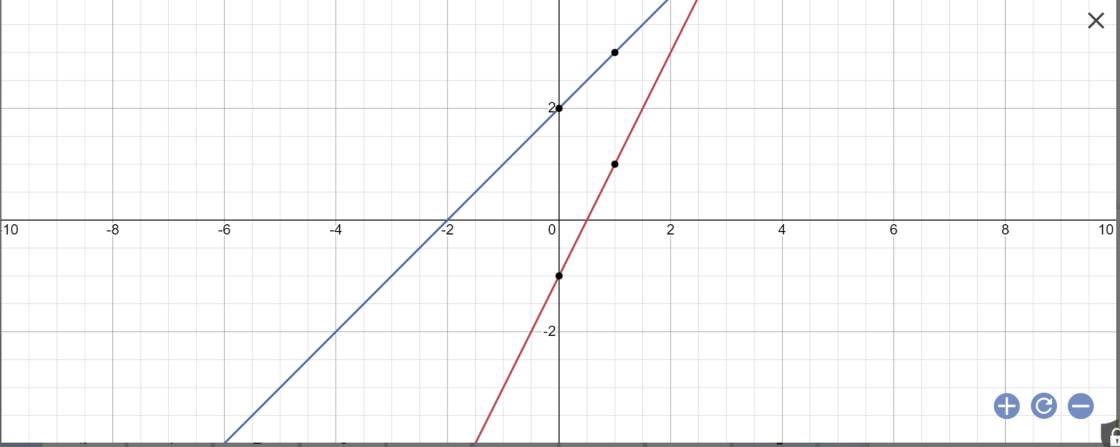 
b: Phương trình hoành độ giao điểm là:
2x-1=x+2
=>x=3
Thay x=3 vào y=x+2, ta được:
y=3+2=5
c: Vì (d)//(d1) nên (d): y=2x+b
Thay x=1 và y=0 vào (d), ta được:
b+2=0
=>b=-2
=>y=2x-2
29 tháng 10 2023
Tọa độ giao điểm của (d2) và (d3) là nghiệm của hệ phương trình sau:
\(\left\{{}\begin{matrix}x+1=-x+3\\y=x+1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x=2\\y=x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
Thay x=1 và y=2 vào (d1), ta được:
\(\left(m^2-1\right)+m^2-5=2\)
=>\(2m^2=8\)
=>\(m^2=4\)
=>\(\left[{}\begin{matrix}m=2\\m=-2\end{matrix}\right.\)
24 tháng 2 2021
1) Ta có: \(\left\{{}\begin{matrix}2\cdot\dfrac{x}{x+2}-\dfrac{y}{y-1}=4\\\dfrac{x}{x+2}-3\cdot\dfrac{y}{y-1}=-3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2\cdot\dfrac{x}{x+2}-\dfrac{y}{y-1}=4\\2\cdot\dfrac{x}{x+2}-6\cdot\dfrac{y}{y-1}=-6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-7\cdot\dfrac{y}{y-1}=10\\2\cdot\dfrac{x}{x+2}-\dfrac{y}{y-1}=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{y}{y-1}=\dfrac{-10}{7}\\2\cdot\dfrac{x}{x+2}+\dfrac{10}{7}=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2\cdot\dfrac{x}{x+2}=\dfrac{18}{7}\\\dfrac{y}{y-1}=\dfrac{-10}{7}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{x+2}=\dfrac{9}{7}\\\dfrac{y}{y-1}=\dfrac{-10}{7}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9\left(x+2\right)=7x\\-10\left(y-1\right)=7y\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}9x+18-7x=0\\-10y+10-7y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+18=0\\-17y+10=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x=-18\\-17y=-10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-9\\y=\dfrac{10}{17}\end{matrix}\right.\)
Vậy: Hệ phương trình có nghiệm duy nhất là \(\left(x,y\right)=\left(-9;\dfrac{10}{17}\right)\)
7 tháng 7 2023
a: d//d1
=>m-2=-m và m+7<>2m-3
=>m=1
b: d trùng với d2
=>m-2=-m^2 và m+7=-2m+1
=>m=-2 và m^2+m-2=0
=>m=-2
d: d vuông góc d4
=>-1/6(m+3)(m-2)=-1
=>(m+3)(m-2)=6
=>m^2+m-6-6=0
=>m^2+m-12=0
=>m=-4 hoặc m=3
c: Thay y=1/3 vào d3, ta được:
-2/3x+5/3=1/3
=>-2/3x=-4/3
=>x=2
Thay x=2 và y=1/3 vào (d), ta được:
2(m-2)+m+7=1/3
=>3m+3=1/3
=>3m=-8/3
=>m=-8/9
Hai đường thẳng:
(d1): (3a – 1)x + 2by = 56 và (d2):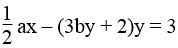
cắt nhau tại điểm M(2; -5) nên tọa độ của M là nghiệm của hệ phương trình: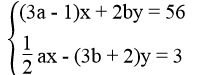 
Thay x = 2, y = -5 vào hệ phương trình, ta có:
Vậy khi a = 8, b = -1 thì hai đường thẳng (d1): (3a – 1)x + 2by = 56 và (d2):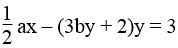
cắt nhau tại điểm M(2; -5).
\((3a-1)x+2by=56(A:3a-1;B:2b)\)(d1)
\(\frac{1}{2}ax-\left(3b+2\right)y=3\left(A:\frac{1}{2}a;B:3b+2\right)\)(d2)
Hai đường thẳng cắt tại điểm M (2;-5) tức là\(x=2,y=-5\) ta thay \(x=2,y=-5\) vào (d1, d2), ta có:
(d1) \(\left(3a-1\right).2+2b.\left(-5\right)=56\\ \Leftrightarrow6a-2-10b=56\\ \Leftrightarrow6a-10b=56+2\\ \Leftrightarrow6a-10b=58\left(1\right)\)
(d2) \(\frac{1}{2}a.2-\left(3b+2\right)\left(-5\right)=3\\ \Leftrightarrow a+15b+10=3\\ \Leftrightarrow a+15b=3-10\\ \Leftrightarrow a+15b=-7\left(2\right)\)
Từ (1) và (2), ta có hệ pt:
\(\left\{{}\begin{matrix}6a-10b=58\\a+15b=-7\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}6a-10b=58\\6a+90b=-42\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}90b-\left(-10\right)b=-42-58\\a+15b=-7\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}100b=-100\\a+15b=-7\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}b=-1\\a+15.\left(-1\right)=-7\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}b=-1\\a-15=-7\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}b=-1\\a=-7+15=8\end{matrix}\right.\)
Vậy giá trị của a và b khi d1, d2 cắt tại M(2;-5) là \(a=8;b=-1\)