Quan sát hình hộp chữ nhật (h.109) và trả lời các câu hỏi sau :

a) Ba đường thẳng nào cắt nhau tại điểm G ?
b) Hai mặt phẳng nào cắt nhau theo đường thẳng FB ?
c) Mặt phẳng (EFBA) và mặt phẳng (FGCB) cắt nhau theo đường thẳng nào ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mặt phẳng (EFBA) và mặt phẳng (FGCB) cắt nhau theo đường thẳng BF.

Mặt phẳng (ABFE) và mặt phẳng (BCGF) cắt nhau theo đường thẳng BF.

a) Những đường thẳng song song với mặt phẳng (ABKI) là A’B’; D’C’; DC; GH.
b) Những đường thẳng vuông góc với mặt phẳng (DCC'D') là A'D'; B'C'; DG; CH; AI; BK.
c) Ta có: A'D' ⊥ (CDD'C') mà A’D’ nằm trong mặt phẳng (A’D’C’B’) nên (A'B'C'D') ⊥ (CDD'C')

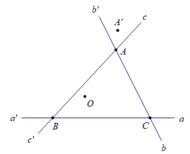
a. Giả sử ba đường thẳng aa’, bb’ và cc’ cắt nhau từng đôi một tại ba điểm A, B, C (hình vẽ). Điểm O cần vẽ là giao điểm của hai tia AO và BO sao cho tia AO nằm giữa hai tia AB và AC, tia BO nằm giữa hai tia BA và BC.
b. Điểm A’ nằm trên tia AA’ sao cho tia AA’ nằm giữa hai tia Ab’ và Ac, A’ và O cùng nằm trong một nửa mặt phẳng có bờ là đường thẳng BC.

a) Ta có: a // a’ mà a’ ⊂ (Q) nên a // (Q);
b // b’ mà b’ ⊂ (Q) nên b // (Q).
Do a // (Q);
b // (Q);
a, b cắt nhau tại M và cùng nằm trong mặt phẳng (P)
Suy ra (P) // (Q).
b) Do (R) // (Q) nên trong mp(R) tồn tại hai đường thẳng a’’, b’’ đi qua M và lần lượt song song với a’, b’ trong mp(Q).
Ta có: a // a’, a’’ // a’ nên a // a’’.
Mà a’’ ∈ (R), do đó a // (R)
Do hai mặt phẳng (P) và (R) có một điểm chung nên chúng có đường thẳng chung d.
Ta có: a // (R);
a ⊂ (P);
(P) ∩ (R) = d.
Suy ra a // d.
Mà a, d cùng nằm trong mặt phẳng (P) và cùng đi qua điểm M nên đường thẳng a chính là giao tuyến của hai mặt phẳng (P) và (R).
Chứng minh tương tự ta cũng có đường thằng b cũng là giao tuyến của hai mặt phẳng (P) và (R).
Như vậy, hai mặt phẳng (P) và (R) có hai giao tuyến a và b nên (P) và (R) là hai mặt phẳng trùng nhau.

a) Những đường thẳng song song với mặt phẳng (ABKI) là DG; CH; A'D'; B'C'; A'B'; D'C'; DC; JH.
b) Những đường thẳng vuông góc với mặt phẳng (DCC'D') là A'D'; B'C'; DG; CH; AI; BK.
c) Ta có: A'D' ⊥ (CDD'C') => (A'B'C'D') \(\perp\) (CDD'C')
a) Những đường thẳng song song với mặt phẳng (ABKI) là : A’B’; D’C’; DC; JH
b) Những đường thẳng vuông góc với mặt phẳng (DCC’D’) là : A’D’; B’C’DJ; CH; AI; BK
c) Hai mặt phẳng (A’B’C’D’) và (CDD’C’) vuông góc với nhau

a: \(mp\left(EFGH\right);mp\left(ABCD\right)\)
\(mp\left(ABFE\right);mp\left(CDHG\right)\)
\(mp\left(ADHE\right);mp\left(BCGF\right)\)
b: Các điểm D,H,G,C cùng thuộc mặt phẳng CDHG
c: Các điểm D,H,G,F không thuộc cùng một mặt phẳng
d: A,B,G,H cùng thuộc mặt phẳng ABGH
a. Ba đường thẳng CG, HG, FG cắt nhau tại G.
b. Mặt phẳng (ABFE) và mặt phẳng (BCGF) cắt nhau theo đường thẳng BF.
c. Mặt phẳng (EFBA) và mặt phẳng (FGCB) cắt nhau theo đường thẳng BF.