Cho tam giác ABC có góc A bằng 70 độ , tia phân giác góc B và góc C cắt nhau tại I , các tia phân giác góc ngoài tại đỉnh B và C cát nhau tại K. Tính các góc của tứ giác BICK
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 6 2019
Ta có:
ICK=ICB+KCB
=1/2ACB+1/2BCx
=1/2 180=90
Hoàn toàn tương tự thì:IBK=90
Xét tứ giác BICK có:
CIB+IBC+ICB+CKB=360
=>CIB=360-(IBC+ICB+CKB)=360-235=125
Vậy các góc của tứ giác BICK là CIB=125, CKB=55
IBK=ICK=90
30 tháng 7 2015
Trong tam giác ABC có góc BAC + ABC + ACB = 180 độ
\(\Rightarrow\) góc ABC + góc ACB = 180 độ - góc BAC = 180 độ - 60 độ = 120 (độ)
Ta có góc IBC + góc ICB = góc ABC/2 + góc ACB/2 = (góc ABC + góc ACB)/2 = 120 độ/2 = 60 (độ)
Trong tam giác IBC có góc BIC + góc IBC + góc ICB = 180 độ
\(\Rightarrow\) góc BIC = 180 độ - (góc IBC + góc ICB) = 180 độ - 60 độ = 120 độ
15 tháng 11 2017
Bạn xem ở đường link này:
Câu hỏi của Cùng học toán đi - Toán lớp 6 - Học toán với OnlineMath
NM
Nguyễn Minh Quang
Giáo viên
6 tháng 11 2020
Hình vẽ a chèn không rõ được không, chắc giống của e thôi.
https://1drv.ms/u/s!AhUPZHs4UJtKilHrVZWqF8i6a584?e=0TIfMP
Ta có : \(\widehat{BIC}=180^0-\widehat{IBC}-\widehat{ICB}\)( Do tổng ba góc trong một tam giác bằng 180 độ)
\(\Rightarrow\widehat{BIC}=180^0-\frac{\widehat{ABC}}{2}-\frac{\widehat{ACB}}{2}\)( Do IB,IC là tia phân giác của góc ABC và ACB)
còn \(\widehat{BKC}=180^0-\widehat{KBC}-\widehat{KCB}\)( Do tổng ba góc trong một tam giác bằng 180 độ)
\(\Rightarrow\widehat{BKC}=180^0-\frac{\widehat{xBC}}{2}-\frac{\widehat{yCB}}{2}\)( Do KB,KC là tia phân giác của góc ABC và ACB)
Mà \(\hept{\begin{cases}\widehat{xBC}=180^0-\widehat{ABC}\\\widehat{yCB}=180^0-\widehat{ACB}\end{cases}}\)\(\Rightarrow\widehat{BKC}=180^0-\left(\frac{180^0-\widehat{ABC}}{2}+\frac{180^0-\widehat{ACB}}{2}\right)\)
\(\Rightarrow\widehat{BKC}=\frac{\widehat{ABC}}{2}+\frac{\widehat{ACB}}{2}\)
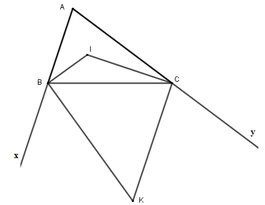
Ta có:
ICK=ICB+KCB
=1/2ACB+1/2BCx
=1/2 180=90
Hoàn toàn tương tự thì:IBK=90
Xét tứ giác BICK có:
CIB+IBC+ICB+CKB=360
=>CIB=360-(IBC+ICB+CKB)=360-235=125
Vậy các góc của tứ giác BICK là CIB=125, CKB=55
IBK=ICK=90
hình bạn tự vẽ nha !chúc bạn học tốt