Cho tam giác ABC và M là trung điểm của BC. Hạ MD, ME theo thứ tự vuông góc với AB và AC. Trên tin BD và CE lần lượt láy các điểm I, K sao cho D là trung điểm của BI, E là trung điểm của CK. Chứng minh 4 điểm B, I, C, K cùng nằm trên một đường tròn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
D
15 tháng 5 2016
1.gọi giao của BD và CE là O
ta có: OB=2/3 BD=> OB=2/3 x 9=6
ta có: OC=2/3 EC=> OC=2/3 x12=8
ta có:\(OC^2+OB^2=6^2+8^2=36+64=100\)
\(BC^2=10^2=100\)
=> tam giác OBC vuông tại O=> BD_|_CE tại O
15 tháng 5 2016
1.gọi giao của BD và CE là O
ta có: OB=2/3 BD=> OB=2/3 x 9=6
ta có: OC=2/3 EC=> OC=2/3 x12=8
ta có:$OC^2+OB^2=6^2+8^2=36+64=100$OC2+OB2=62+82=36+64=100
$BC^2=10^2=100$BC2=102=100
=> tam giác OBC vuông tại O=> BD_|_CE tại O
27 tháng 8 2017
câu a
Gọi H là chân đường vuông góc hạ từ M xuống tia phân giác ^BAC. Tam giác ADE có AH vừa là phân giác vùa là đường cao nên cân tại A.
Qua B vẽ BF//CE (F thuộc DE) => tam giác BDF cân tại B => BD = BF (1)
Mặt khác xét 2 tam giác BMF và CME có : BM = CM; ^BMF = ^CME ( đối đỉnh); ^MBF = ^MCE ( so le trong) => tam giác BMF = tg CME => BF = CE (2)
Từ (1) và (2) => đpcm
mấy câu còn lại bó tay
4 tháng 1 2022
a: Xét tứ giác ABEC có
M là trung điểm của BC
M là trung điểm của AE
Do đó: ABEC là hình bình hành
Suy ra: AB=CE
c: Ta có: ABEC là hình bình hành
nên \(\widehat{BAC}=\widehat{BEC}\)
CM
9 tháng 3 2019
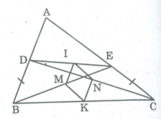
*Trong ∆ BCD,ta có:
K là trung điểm của BC (gt)
N là trung điểm của CD (gt)
Nên NK là đường trung bình của ∆ BCD
⇒ NK // BD và NK = 1/2 BD (1)
*Trong ∆ BED,ta có:
M là trung điểm của BE (gt)
I là trung điểm của DE (gt)
Nên MI là đường trung bình của ∆ BED
⇒ MI // BD và MI = 1/2 BD (t/chất đường trung bình trong tam giác) (2)
Từ (1) và (2) suy ra: MI // NK và MI = NK
Nên tứ giác MKNI là hình bình hành.
*Trong ∆ BEC ta có MK là đường trung bình.
⇒ MK = 1/2 CE (t/chất đường trung bình của tam giác)
BD = CE (gt). Suy ra: MK = KN
Vậy hình bình hành MKNI là hình thoi.
⇒IK ⊥ MN (t/chất hình thoi).