Mọi người ơi giúp em với, em phải nộp bây giờ mà không biết cách làm 😭😭
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TT
2
Những câu hỏi liên quan
TP
15 tháng 7 2021
Bài 1:
Ta có : 1 mol muối RCO3 (có khối lượng = R + 60n) chuyển thành 1 mol RCln (có khối lượng = R + 71n)
=> khối lượng tăng = 71n – 60n = 11n gam
=> Khi chuyển 1 mol gốc CO3 thành 2 mol gốc Cl và tạo ra 1 mol CO2 thì khối lượng tăng 11 gam
a) Ta có công thức tính nhanh sau : \(m_{muốiclorua}=n_{muốicacbonat}+11.n_{CO_2}\)
=> \(n_{CO_2}=\dfrac{11,1-10}{11}=0,1\left(mol\right)\)
=> \(V_{CO_2}=0,1.22,4=2,24\left(l\right)\)
b) \(MCO_3+2HCl\rightarrow MCl_2+CO_2+H_2O\)
\(n_{HCl}=2n_{CO_2}=0,2\left(mol\right)\)
=> \(m_{ddHCl}=\dfrac{0,2.36,5}{3,65\%}=200\left(g\right)\)
c) \(m_{ddsaupu}=10+200-0,1.44=205,6\left(g\right)\)
\(C\%_{muối}=\dfrac{11,1}{205,6}.100=5,4\%\)
d) \(n_{MCO_3}=n_{MCl_2}\)
=> \(\dfrac{10}{M+60}=\dfrac{11,1}{M+71}\)
=> \(M=40\left(Ca\right)\)
HP
1
12 tháng 12 2018
Gọi số hoa của 3 bạn lần lượt là x, y , z
Vì x,y,z TLT vớ 4,5,6
=> x/4=y/5=z/6=k
Theo t/c dãy tỉ số bằng nhau :
k= x+y+z/ 4+5+6 = 75/15=5
=> x= 5.4=20
y= 5. 5 = 25
z= 5.6=30
Vậy ..
BN
12 tháng 12 2018
Gọi số hoa 3 bạn hái được lần lượt là a,b,c \(\left(a,b,c\inℕ^∗\right)\)
Theo đề bài ra,ta có :
\(\frac{a}{4}=\frac{b}{5}=\frac{c}{6}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ,ta có :
\(\frac{a}{4}=\frac{b}{5}=\frac{c}{6}=\frac{a+b+c}{4+5+6}=\frac{75}{15}=6\)
\(\Rightarrow\hept{\begin{cases}a=6.4=24\\b=6.5=30\\c=6.6=36\end{cases}}\)
Vậy ....
2 tháng 10 2021
8: Ta có: \(\sqrt{6+2\sqrt{5}}-\dfrac{\sqrt{15}-\sqrt{3}}{\sqrt{3}}\)
\(=\sqrt{5}+1-\sqrt{5}+1\)
=2
2 tháng 10 2021
a: Xét ΔAHD có
AP là đường cao ứng với cạnh HD
AP là đường trung tuyến ứng với cạnh HD
Do đó: ΔAHD cân tại A
mà AP là đường cao ứng với cạnh HD
nên AP là đường phân giác ứng với cạnh HD
Xét ΔAHE có
AQ là đường cao ứng với cạnh HE
AQ là đường trung tuyến ứng với cạnh HE
Do đó: ΔHAE cân tại A
mà AQ là đường cao ứng với cạnh HE
nên AQ là đường phân giác ứng với cạnh HE
Ta có: \(\widehat{EAD}=\widehat{EAH}+\widehat{DAH}\)
\(=2\left(\widehat{QAH}+\widehat{PAH}\right)\)
\(=2\cdot90^0=180^0\)
Do đó: E,A,D thẳng hàng
mà AD=AE(=AH)
nên A là trung điểm của DE
2 tháng 10 2021
a) Xét \(\Delta ADP\) = \(\Delta AHP\) có: ( cạnh huyền -cạnh góc vuông)
góc APD = APH=90o
AD = AH
AP chung
=> AD=AH (1)
CMTT với \(\Delta AEQ=\Delta AHQ\left(CH-CGV\right)\)
=> AE= AH (2)
Từ 1 và 2 => AD= AE
=> A là trung điểm của DE
b) Xét \(\Delta DHE\) có:
DP=PH; HQ=QE
=> PQ là đg trung bình của tam giắc DHE
=> PQ// DE; PQ=1/2 DE
c) Xét tứ giác APHQ có: góc HPA= 90o; Góc A =90o; góc HQA=90o
=> Tứ giác APHQ là HCN
=> PQ=AH ( theo t/c HCN)
10 tháng 10 2021
d: ta có: \(C=3+3^3+3^5+...+3^{1991}\)
\(=3\left(1+3^2+3^4\right)+...+3^{1987}\left(1+3^2+3^4\right)\)
\(=91\cdot\left(3+...+3^{1987}\right)⋮13\)
ML
0
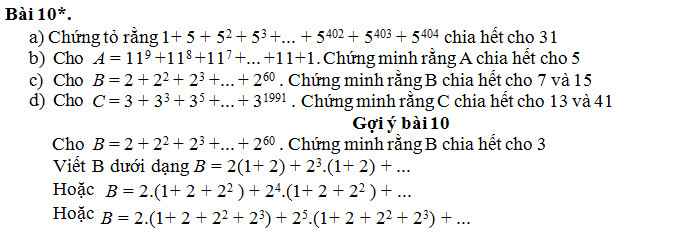
\(\left(3x+1\right)^2=9x^2+6x+1\)
\(\left(-4+x\right)^2=16-8x+x^2\)
\(9+12x+4x^2=\left(3+2x\right)^2\)
d giống a, e giống b (đề bị lặp)
a: \(\left(3x+1\right)^2=9x^2+6x+1\)
b: \(\left(-4+x\right)^2=16-8x+x^2\)
c: \(9+12x+4x^2=\left(3+2x\right)^2\)
d: \(\left(3x+1\right)^2=9x^2+6x+1\)
e: \(\left(-4+x\right)^2=16-8x+x^2\)