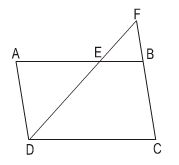
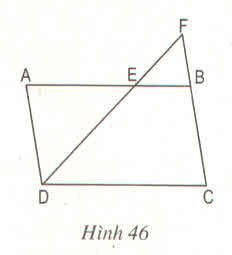
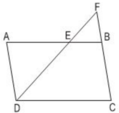
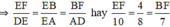Cho hình bình hành ABCD (h.46) có độ dài các cạnh AB = 12cm, BC = 7cm. Trên cạnh AB lấy một điểm E sao cho AE = 8cm. Đường thẳng DE cắt cạnh CB kéo dài tại F
a) Trong hình vẽ đã cho có bao nhiêu cặp tam giác đồng dạng với nhau ? Hãy viết các cặp tam giác đồng dạng với nhau theo các đỉnh tương ứng ?
b) Tính độ dài các đoạn thẳng EF và BF, biết rằng DE = 10 cm

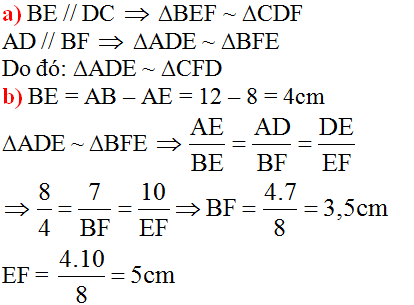
 ΔFDC (1)
ΔFDC (1) ΔDEA (2)
ΔDEA (2) ΔFDC (tính chất)
ΔFDC (tính chất)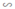 ΔDEA
ΔDEA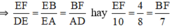
 ΔFDC (1)
ΔFDC (1) ΔDEA (2)
ΔDEA (2) ΔFDC (tính chất)
ΔFDC (tính chất) ΔDEA
ΔDEA