Cho P(x) =x3-3mx +m2
Q(x)= x2 +(3m +2) x+m2
Tìm giá trị của m sao cho P(-1) = Q(2)
Giúp mìk nha
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TH
1
5 tháng 3 2022
\(H\left(-1\right)=K\left(2\right)\Rightarrow-1+3m+m^2=4+2\left(3m+2\right)+m^2\)
\(\Leftrightarrow-1+3m=8+6m\Leftrightarrow3m=-9\Leftrightarrow m=-3\)
CM
17 tháng 11 2018
Thay x = −3 vào phương trình
(m – 2)x2 – (m2 + 1)x + 3m = 0, ta có:
(m – 2) (−3)2 – (m2 + 1) (−3) + 3m = 0
⇔ 9m – 18 + 3m2 + 3 + 3m = 0
⇔ 3m2 + 12m – 15 = 0
⇔ m2 + 4m – 5 = 0
⇔ m2 – m + 5m – 5 = 0
⇔ m (m – 1) + 5 (m – 1) = 0
⇔ (m – 1) (m + 5) = 0 ⇔ m = 1 m = − 5
Suy ra tổng các giá trị của m là (−5) + 1 = −4
Đáp án cần chọn là: B
.
.
.
.
CM
14 tháng 2 2017
Chọn D
.
Hàm số đạt cực tiểu tại 
.
Phương trình vô nghiệm.
Vậy không tìm được 
thỏa mãn yêu cầu bài toán.
CM
3 tháng 7 2019
Chọn A
Ta có y ' = 3 x 2 + 4 ( m - 1 ) x + m 2 - 4 m + 1 . Hàm số có hai cực trị
=> y' = 0 có hai nghiệm phân biệt <=> Δ' > 0 <=> 4 ( m - 1 ) 2 - 3 ( m 2 - 4 m + 1 ) > 0
<=> m 2 + 4 m + 1 > 0
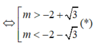
Áp dụng Vi-ét cho phương trình y’ = 0 có hai nghiệm phân biệt x 1 , x 2 ta có
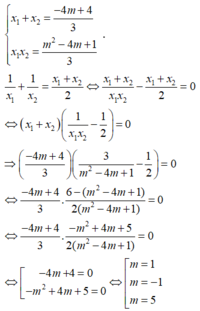
Đối chiếu điều kiện (*) có m = 5 hoặc m = 1
CM
19 tháng 12 2018
a) y′ = 3 x 2 + 2(m + 3)x + m
y′ = 0 ⇔ 3 x 2 + 2(m + 3)x + m = 0
Hàm số đạt cực trị tại x = 1 thì:
y′(1) = 3 + 2(m + 3) + m = 3m + 9 = 0 ⇔ m = −3
Khi đó,
y′ = 3 x 2 – 3;
y′′ = 6x;
y′′(1) = 6 > 0;
Suy ra hàm số đạt cực tiểu tại x = 1 khi m = 3.
b) y′ = −( m 2 + 6m) x 2 − 4mx + 3
y′(−1) = − m 2 − 6m + 4m + 3 = (− m 2 − 2m – 1) + 4 = −(m + 1)2 + 4
Hàm số đạt cực trị tại x = -1 thì :
y′(−1) = − ( m + 1 ) 2 + 4 = 0 ⇔ ( m + 1 ) 2 = 4
⇔ 
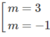
Với m = -3 ta có y’ = 9 x 2 + 12x + 3
⇒ y′′ = 18x + 12
⇒ y′′(−1) = −18 + 12 = −6 < 0
Suy ra hàm số đạt cực đại tại x = -1.
Với m = 1 ta có:
y′ = −7 x 2 − 4x + 3
⇒ y′′ = −14x − 4
⇒ y′′(−1) = 10 > 0
Suy ra hàm số đạt cực tiểu tại x = -1
Kết luận: Hàm số đã cho đạt cực đại tại x = -1 khi m = -3.
Cho P(x) =x3 -3mx +m2
Q(x)= x2 +(3m +2) x+m2
Tìm giá trị của m sao cho P(-1) = Q(2)
P(-1) = (-1)3 - 3m.(-1) + m2 = -1 + 3m + m2
Q(2) = 22 + ( 3.m + 2) . 2 + m2 = 8 + 6m + m2
P(-1) = Q(2) \(\Rightarrow\) -1 + 3m + m2 = 8 + 6m + m2
\(\Rightarrow\) -1 + 3m = 8 + 6m + m2 - m2
\(\Rightarrow\) -1 + 3m = 8 + 6m
\(\Rightarrow\) 3m - 6m = 1+8
=> -3m = 9
=> m = -3
Vậy m= -3 thì P(-1) = Q(2)