Hãy chỉ ra một nghiệm của bất phương trình trong ví dụ của câu hỏi 2 ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QT
1
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
a) \(\left\{ \begin{array}{l}3x + y - 1 \le 0\\2x - y + 2 \ge 0\end{array} \right.\)
Cặp số \((0;0)\) là một nghiệm của hệ bất phương trình trên vì \(\left\{ \begin{array}{l}3.0 + 0 - 1 = - 1 \le 0\\2.0 - 0 + 2 = 2 \ge 0\end{array} \right.\)
Cặp số \((0; - 1)\) là một nghiệm của hệ bất phương trình trên vì \(\left\{ \begin{array}{l}3.0 + ( - 1) - 1 = - 2 \le 0\\2.0 - ( - 1) + 2 = 3 \ge 0\end{array} \right.\)
c) \(\left\{ \begin{array}{l}y - 1 < 0\\x + 2 \ge 0\end{array} \right.\)
Cặp số \((0;0)\) là một nghiệm của hệ bất phương trình trên vì \(\left\{ \begin{array}{l}0 - 1 = - 1 < 0\\0 + 2 = 2 \ge 0\end{array} \right.\)
Cặp số \((1;0)\) là một nghiệm của hệ bất phương trình trên vì \(\left\{ \begin{array}{l}0 - 1 = - 1 < 0\\1 + 2 = 3 \ge 0\end{array} \right.\)
d) \(\left\{ \begin{array}{l}x + y - 3 \le 0\\ - 2x + y + 3 \ge 0\\x \ge 0\\y \ge 0\end{array} \right.\)
Cặp số \((0;0)\) là một nghiệm của hệ bất phương trình trên vì \(\left\{ \begin{array}{l}0 + 0 - 3 = - 3 \le 0\\ - 2.0 + 0 + 3 = 3 \ge 0\\0 \ge 0\\0 \ge 0\end{array} \right.\)
Cặp số \((0;1)\) là một nghiệm của hệ bất phương trình trên vì \(\left\{ \begin{array}{l}0 + 1 - 3 = - 2 \le 0\\ - 2.0 + 1 + 3 = 4 \ge 0\\0 \ge 0\\1 \ge 0\end{array} \right.\)
CM
8 tháng 6 2019
2x + 3 ≥ -6
Vế trái của bất phương trình: 2x + 3
Vế phải của bất phương trình: -6
PT
1
CM
1 tháng 4 2018
2x + 4 < 0
⇔ 2x < -4 ⇔ x < -2
Ví dụ -3 là một nghiệm của bất phương trình này.
24 tháng 5 2021
Tham khảo :
Câu 1 :
Danh từ : Con mèo .
VD : Nhà em mới mua một con mèo tam thể rất đẹp .
Động từ : Học võ .
Bạn Linh rất thích học võ .
Tính từ : Rực rỡ .
VD : Những bông hoa đang nở rực rỡ .
Câu 2 :
Nàng ca sĩ họa mi đang cất lên những tiếng hát trong trẻo .
Phép tu từ : Nhân hóa .
Câu 3 :
Qua bao thời gian, giờ đây, mẹ đã ngoài ba mươi tuổi nhưng trông mẹ tôi vẫn còn rất trẻ lắm. Thời gian trôi qua, những gánh nặng vất vả của cuộc giống làm phai màu tóc mẹ. Đôi vai gầy ấy đã gánh vác biết bao điều để lo toan cho cuộc sống của chị em tôi. Khuôn mặt trái xoan của mẹ luôn tạo nên sự gần gũi , thân thiện . Bởi vậy , trong công việc, hầu như ai cũng yêu quý mẹ. Tôi chẳng thể quên được đôi bàn tay đầy vết chai sạn; đã dạy cho tôi những nét chữ đầu tiên, dìu dắt tôi bước đầu trên đường đời. Mẹ tôi tần tảo sớm hôm chăm lo cho tôi và gia đình nhỏ, mỗi khi đi làm về dù rất mệt nhưng mẹ vẫn phải nấu cơm. Tôi nhớ nhất một hôm, lúc nào đó vào buổi tối, mẹ bảo tôi đi ngủ, tôi chỉ lên gường và giả vờ ngủ. Vì mẹ tôi là thợ may, nên để kiếm thêm thu nhập, mỗi tối mẹ thường nhận thêm công việc sửa chữa quần áo. Từ ánh đèn hắt ra, mẹ tôi ngồi đó, tay đưa chỉ, tiếng bàn đạp từ máy khâu vang lên nhịp nhàng đều đều trong đêm vắng. Nhìn cảnh tượng đó tôi chợt nhớ tới câu thơ tôi từng đọc:" Tôi hoảng sợ ngày bàn tay mẹ mỏi/ Mình vẫn còn một thứ quả non xanh?" và lòng thầm tự hứa với mẹ, con sẽ trở thành đứa con ngoan trò giỏi để không phụ công ơn của mẹ.
PP
24 tháng 5 2021
Tham khảo nhé:
1. Danh từ: Cái quạt
Động từ:chạy
Tính từ: Đẹp
2. Tiếng suối trong như tiếng hát xa
Biện pháp nghệ thuật: Só sánh
3.
Trong gia đình em, người mà em yêu quý và kính trọng nhất là mẹ.
Năm nay, mẹ ba sáu tuổi. Dáng người thon thả. Mái tóc dài mượt mà và óng ả. Khuôn mặt trái xoan. Đôi mắt mẹ sáng long lanh như ngọn đuốc dõi theo từng bước đi của em. Môi mẹ đỏ tươi, luôn in lại những nụ cười rạng rỡ. Làn da của mẹ trắng mịn như được thoa một lớp phấn. Mẹ ăn mặc rất giản dị nhưng lại toát lên vẻ sang trọng. Hằng ngày, ngoài những công việc giảng dạy ở trường và tham gia các công tác đoàn thể mẹ còn phải lo chăm sóc chu đáo cho gia đình. Tối đến, dù bận soạn bài nhưng mẹ vẫn dành thời gian giảng bài cho em. Những hôm em ốm, nhờ có bàn tay mẹ chăm sóc mà em đã nhanh khỏi để đến trường. Hằng ngày, mẹ phải dậy sớm để lo bữa sáng cho gia đình. Công việc bận rộn như vậy nhưng lúc nào mẹ cũng rất vui. Mẹ không những là người mẹ dịu dàng, đảm đang mà mẹ vừa là người chị, người bạn của em những lúc vui buồn. Có mẹ, em thấy ấm lòng. Em rất kính trọng mẹ em, mẹ xứng đáng là người "Giỏi việc trường, đảm việc nhà" mà nhà trường đã trao tặng danh hiệu cho mẹ trong công tác.
Em rất yêu quý mẹ em. Em sẽ cố gắng học giỏi để xứng đáng với công sinh thành và nuôi dưỡng của mẹ.
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
a) \(5x + 3y < 20\)
Đây là bất phương trình bậc nhất hai ẩn.
Chọn \(x = 0;y = 0\)
Khi đó bất phương trình tương đương với 5.0+3.0
Vậy (0;0) là một nghiệm của bất phương trình trên.
b) \(3x - \frac{5}{y} > 2\)
Đây không là bất phương trình bậc nhất hai ẩn vì có ẩn y ở mẫu.
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
a) Ví dụ:
\(\begin{array}{l}{x^2} - x + 1 > 0\\ - {x^2} + 5x + 5 \le 0\end{array}\)
b)
Bất phương trình bậc nhất: \(x - 1 > 0\)
Bất phương trình hai ẩn: \(2x + y < 5\)
24 tháng 9 2023
Tham khảo:
a) Vì \(0 - 2.0 + 6 = 6 > 0\) nên (0;0) là một nghiệm của bất phương trình đã cho.
b) Vì \(0 - 2.1 + 6 = 4 > 0\) nên (0;1) là một nghiệm của bất phương trình đã cho.
Vì \(1 - 2.0 + 6 = 7 > 0\) nên (1;0) là một nghiệm của bất phương trình đã cho.
Vì \(1 - 2.1 + 6 = 5 > 0\) nên (1;1) là một nghiệm của bất phương trình đã cho.
c) Vẽ đường thẳng \(\Delta :x - 2y + 6 = 0\) đi qua hai điểm \(A(0;3)\) và \(B\left( { - 2;2} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \(0 - 2.0 + 6 = 6 > 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ \(\Delta \), chứa gốc tọa độ O
(miền không gạch chéo trên hình)
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
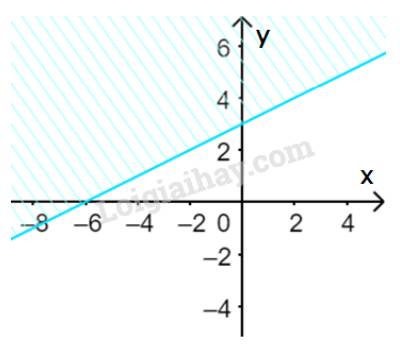
a)
+) Thay x=0 và y=0 vào bất phương trình \(x + 2y \ge 0\), ta được:
\(0 + 2.0 \ge 0 \Leftrightarrow 0 \ge 0\)(Đúng)
=> (0;0) là một nghiệm của bất phương trình \(x + 2y \ge 0\)
+) Thay x=1, y=1 vào bất phương trình \(x + 2y \ge 0\) ta được:
\(1 + 2.1 \ge 0 \Leftrightarrow 3 \ge 0\)(Đúng)
=> (1;1) là một nghiệm của bất phương trình \(x + 2y \ge 0\)
Ta tìm được 2 nghiệm của bất phương trình đã cho là (0;0) và (1;1).
b)
Thay y=0 vào bất phương trình \(x + 2y \ge 0\) ta được:
\(x + 2.0 \ge 0 \Leftrightarrow x \ge 0\)
Ta thấy bất phương trình bài cho tương đương với bất phương trình nên số giá trị của x thỏa mãn bất phương trình đã cho là số x thỏa mãn điều kiện .
Mà ta có vô số giá trị của x thỏa mãn nên có vô số giá trị của x thỏa mãn bất phương trình đã cho.
Chú ý
Ta có thể thử các cặp số khác đối với câu a, miễn là cặp số đấy làm cho bất phương trình đúng.
Ví dụ: 2x + 4 < 0
⇔ 2x < -4 ⇔ x < -2
Ví dụ -3 là một nghiệm của bất phương trình này.