Cho \(\Delta ABC=\Delta HIK\)
a) Tìm cạnh tương ứng với cạnh BC. Tìm góc tương ứng với góc H
b) Tìm các cạnh bằng nhau, tìm các góc bằng nhau
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Cạnh tương ứng với cạnh BC là IK
Góc tương ứng với góc H là góc A
b) Các cạnh bằng nhau: AB và HI; AC và HK; BC và IK
Các góc bằng nhau: góc A và góc H; góc B và góc I; góc C và góc K

a) Cạnh tương ứng với AC là HK
Góc tương ứng với góc I là góc B
b) Các cạnh bằng nhau: AB = HI ; BC = IK; AC = HK
Các góc bằng nhau: góc A = góc H; góc B = góc I; góc C = góc K
xét \(\Delta ABC\) và \(\Delta HIK\)
a) cạnh tương ứng với cạnh \(AC\)là \(HK\)
góc tương ứng với góc \(I\)là góc \(B\)
b) các cạnh = nhau: \(AB=HI\); \(AC=HK\); \(BC=IK\)
các góc = nhau \(\widehat{A}=\widehat{H}\); \(\widehat{B}=\widehat{I}\); \(\widehat{C}=\widehat{K}\)

1 a,Ta có ∆ ABC= ∆ HIK, nên cạnh tương ứng với BC là cạnh IK
góc tương ứng với góc H là góc A.
ta có : ∆ ABC= ∆ HIK
Suy ra: AB=HI, AC=HK, BC=IK.
=
,
=
,
=
.
b,
∆ ABC= ∆HIK
Suy ra: AB=HI=2cm, BC=IK=6cm, =
=400
2.
Ta có ∆ABC= ∆ DEF
Suy ra: AB=DE=4cm, BC=EF=6cm, DF=AC=5cm.
Chu vi của tam giác ABC bằng: AB+BC+AC= 4+5+6=15 (cm)
Chu vi của tam giác DEF bằng: DE+EF+DF= 4+5+6=15 (cm

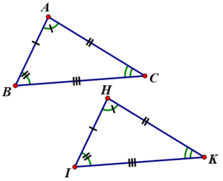
a) Vì tam giác ABC = tam giác HIK nên
- Cạnh tương ứng với cạnh BC là IK
- Góc tương ứng với góc H là góc A

Vì \(\widehat A = \widehat E\), \(\widehat C = \widehat D\) nên đỉnh A tương ứng với đỉnh E, đỉnh C tương ứng với đỉnh D.
\( \Rightarrow \widehat B = \widehat F\) ( 2 góc tương ứng)
Do đó, \(\Delta{ABC}=\Delta{EFD}\)
\(\Rightarrow AB = DE;BC = EF;AC = DF\)( các cạnh tương ứng )
a) Vì \(\Delta ABC=\Delta HIK\)
nên BC = IK (2 cạnh t/ư)
và \(\widehat{A}=\widehat{H}\) (2 góc t/ư)
b) Do \(\Delta ABC=\Delta HIK\)
=> AB = HI; AC = HK (2 cạnh t.ư); BC = IK (câu a)
và \(\widehat{A}=\widehat{H}\) (câu a); \(\widehat{B}=\widehat{I}\) và \(\widehat{C}=\widehat{K}\) (2 góc t/ư).
a) Ta có \(\Delta\) ABC= \(\Delta\)HIK, nên cạnh tương ứng với BC là cạnh IK
góc tương ứng với góc H là góc A.
b) \(\Delta\) ABC= \(\Delta\)HIK
Suy ra: AB=HI, AC=HK, BC=IK.
\(\widehat{A}=\widehat{H};\widehat{B}=\widehat{I};\widehat{C}=\widehat{K}\)