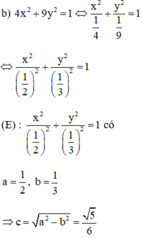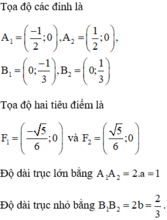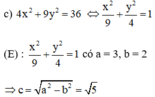Cho một elip (E) : \(x^2+4y^2=16\)
a) Xác định tọa độ các tiêu điểm và các đỉnh của elip (E)
b) Viết phương trình đường thẳng \(\Delta\) đi qua điểm \(M\left(1;\dfrac{1}{2}\right)\) và có vectơ pháp tuyến \(\overrightarrow{n}=\left(1;2\right)\)
c) Tìm tọa độ các giao điểm A và B của đường thẳng \(\Delta\) và elip (E). Chứng minh MA = MB


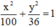 có a = 10; b = 6 ⇒ c
có a = 10; b = 6 ⇒ c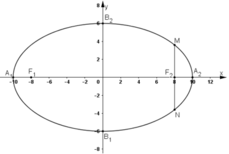
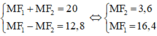
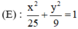 có a = 5, b = 3 ⇒ c = √(a
có a = 5, b = 3 ⇒ c = √(a