Cho hai hình bình hành ABCD và EBEF với A, D, F không thẳng hàng. Dựng các vectơ \(\overrightarrow{EH}\) và \(\overrightarrow{FG}\) bằng vectơ \(\overrightarrow{AD}\). Chứng minh tứ giác CDGH là hình bình hành ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
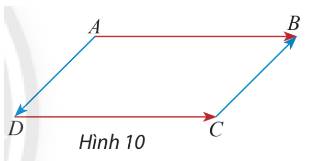
a) Ta có: \(AB = CD \Rightarrow \left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {CD} } \right|\)
\(AB//CD\) và \(\overrightarrow {AB} \), \(\overrightarrow {DC} \) có hướng từ trái sang phải
Suy ra \(\overrightarrow {AB} \) và \(\overrightarrow {DC} \) cùng hướng
b) Ta có: \(AD = CB \Rightarrow \left| {\overrightarrow {AD} } \right| = \left| {\overrightarrow {CB} } \right|\)
\(AD//CB\) và \(\overrightarrow {AD} \)có hướng từ trên xuống dưới, \(\overrightarrow {CB} \) có hướng từ dưới lên trên. Suy ra \(\overrightarrow {AD} \) và \(\overrightarrow {CB} \) ngược hướng
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
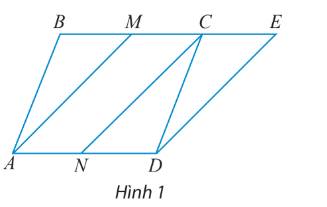
a) Ta có: \(\overrightarrow {CE} = \overrightarrow {AN} \Rightarrow CE//AN\) và \(CE = AN = ND = BM = MC\)
Suy ra \(\overrightarrow {MC} = \overrightarrow {CE} \)
+) \(\overrightarrow {NC} + \overrightarrow {MC} = \overrightarrow {NC} + \overrightarrow {CE} = \overrightarrow {NE} \)
+) ABCD là hình bình hành nên \(\overrightarrow {CD} = \overrightarrow {BA} \)
\(\overrightarrow {AM} + \overrightarrow {CD} = \overrightarrow {AM} + \overrightarrow {BA} = \overrightarrow {BM} \)
+) Ta có \(\overrightarrow {MC} = \overrightarrow {AN} \Rightarrow AMCN\) là hình bình hành nên \(\overrightarrow {NC} = \overrightarrow {AM} \)
\(\overrightarrow {AD} + \overrightarrow {NC} = \overrightarrow {AD} + \overrightarrow {AM} = \overrightarrow {AE} \) (vì AMED là hình bình hành)
b) Ta có:
+) \(\overrightarrow {NC} - \overrightarrow {MC} = \overrightarrow {NC} + \overrightarrow {CM} = \overrightarrow {NM} \)
+) \(\overrightarrow {AC} - \overrightarrow {BC} = \overrightarrow {AC} + \overrightarrow {CB} = \overrightarrow {AB} \)
+) \(\overrightarrow {AB} - \overrightarrow {ME} = \overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {DA} = \overrightarrow {DB} \)
c) Ta có:
\(\overrightarrow {AM} + \overrightarrow {AN} = \overrightarrow {AM} + \overrightarrow {MC} = \overrightarrow {AC} \)
Áp dụng quy tắc hình bình hành vào hình bình hành ABCD ta có
\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
Từ đó suy ra \(\overrightarrow {AM} + \overrightarrow {AN} = \overrightarrow {AB} + \overrightarrow {AD} \) (đpcm)
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
Vì ABCD là hình bình hành nên \(\left\{ \begin{array}{l}AD//\;BC\\AD = BC\end{array} \right.\), hay \(\overrightarrow {AD} = \overrightarrow {BC} \).
Do đó \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \).
BT
18 tháng 5 2017
a)
Các véc tơ cùng phương với \(\overrightarrow{AB}\) là:
\(\overrightarrow{MO};\overrightarrow{OM};\overrightarrow{MN};\overrightarrow{NM};\overrightarrow{NO};\overrightarrow{ON};\overrightarrow{DC};\overrightarrow{CD};\overrightarrow{BA};\overrightarrow{AB}\).
Hai véc tơ cùng hướng với \(\overrightarrow{AB}\) là:
\(\overrightarrow{MO};\overrightarrow{ON}\).
Hai véc tơ ngược hướng với \(\overrightarrow{AB}\) là:
\(\overrightarrow{OM};\overrightarrow{ON}\).
b) Một véc tơ bằng véc tơ \(\overrightarrow{MO}\) là: \(\overrightarrow{ON}\).
Một véc tơ bằng véc tơ \(\overrightarrow{OB}\) là: \(\overrightarrow{DO}\).
24 tháng 9 2023
Tham khảo:
Ta có: \( \overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \) (do ABCD là hình bình hành)
\( \Rightarrow \overrightarrow {BM} = \overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
\( \Rightarrow \) Tứ giác ABMC là hình bình hành.
\( \Rightarrow \overrightarrow {DC} =\overrightarrow {AB} = \overrightarrow {CM} \).
\( \Rightarrow C\) là trung điểm DM.
Vậy M thuộc DC sao cho C là trung điểm DM.
Chú ý khi giải
+) Tứ giác ABCD là hình bình hành \( \Leftrightarrow \overrightarrow {AD} = \overrightarrow {BC} \)
+) ABCD là hình bình hành thì \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
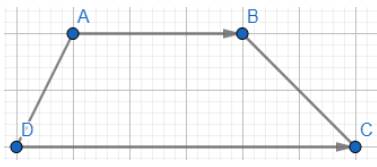
Áp dụng quy tắc ba điểm ta có:
\(\overrightarrow a = \overrightarrow {AC} + \overrightarrow {CB} = \overrightarrow {AB} \); \(\overrightarrow b = \overrightarrow {DB} + \overrightarrow {BC} = \overrightarrow {DC} \)
Mà ABCD là hình thang nên AB//DC. Mặt khác vectơ \(\overrightarrow {AB} \) và vectơ \(\overrightarrow {DC} \) đều có hướng từ trái sang phải, suy ra vectơ \(\overrightarrow {AB} \) và vectơ \(\overrightarrow {DC} \)cùng hướng
Vậy hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng.
\(\overrightarrow{EH}=\overrightarrow{AD},\overrightarrow{FG}=\overrightarrow{AD}\Rightarrow\overrightarrow{EH}=\overrightarrow{FG}\)
=> Tứ giác FEHG là hình bình hành
=> \(\overrightarrow{GH}=\overrightarrow{FE}\) (1)
Ta có \(\overrightarrow{DC}=\overrightarrow{AB},\overrightarrow{AB}=\overrightarrow{FE}\)
=> \(\overrightarrow{DC}=\overrightarrow{FE}\) (2)
Từ (1) và (2) ta có \(\overrightarrow{GH}=\overrightarrow{DC}\)
Vậy tứ giác GHCD là hình bình hành.