Trong mặt phẳng, cho 6 điểm phân biệt sao cho không có 3 điểm nào thẳng hành. Hỏi có thể lập được bao nhiêu tam giác mà các đỉnh của nó thuộc tập điểm đã cho ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
25 tháng 3 2019
Đáp án là B
Cứ 3 điểm phân biệt không thẳng hàng tạo thành một tam giác.
Lấy 3 điểm bất kỳ trong 6 điểm phân biệt thì số tam giác cần tìm chính là một tổ hợp chập 3 của 6 phần tử (điểm).
Như vậy, ta có C 6 3 = 20 tam giác.
CM
30 tháng 5 2018
Cứ chọn 3 điểm không thẳng hàng bất kì ta được một tam giác.
Việc lập các tam giác chính là chọn 3 điểm trong tập hợp 6 điểm đã cho và chính là tổ hợp chập 3 của 6.
Vậy có:
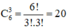cách lập.
CM
9 tháng 9 2019
- Chọn 3 điểm trong 18 điểm đã cho làm 3 đỉnh của một tam giác. Mỗi tam giác là một tổ hợp chập 3 của 18. Vì vậy số tam giác là C183 (chọn phương án B)
CM
2 tháng 1 2020
Chọn A
Ta chọn bất kì 3 điểm trong 18 điểm đã cho thì tạo thành một tam giác.
Do đó số tam giác được tạo thành là số cách chọn 3 điểm phân biệt bất kỳ (không kể thứ tự) từ 18 điểm đã cho.
Vậy có tất C 18 3 tam giác.
WW
26 tháng 6 2017
Lời giải:
a/ Cố định 1 điểm trong 6 điểm này, nối điểm này với 5 điểm còn lại ta được 5 đoạn thẳng.
Có 6 điểm như vậy nên có tất cả 6 . 5 = 30 (đoạn thẳng).
Nhưng mỗi đoạn thẳng đã được tính 2 lần nên số các đoạn thẳng tạo được từ 12 điểm này là 30 : 2 = 15 (đoạn thẳng).
b/
Với một đoạn thẳng, nối 2 đầu của đoạn thẳng này với 1 điểm khác ta được một tam giác.
Cố định 1 đoạn thẳng trong 15 đoạn thẳng, nối hai đầu của đoạn thẳng này với 4 điểm còn lại ta được 4 tam giác. Có 15 đoạn thẳng như vậy nên có tất cả 15 .4 = 60 (tam giác).
Nhưng mỗi tam giác đã được tính 3 lần nên số các tam giác tạo được từ 6 điểm này là 60 : 3 = 20 (tam giác).
Chúc bạn học tốt, thân!
Mỗi tập con gồm 3 điểm (không phân biệt thứ tự) của tập hợp 6 điểm đã cho xác định duy nhất một tam giác. Từ đó ta có: số tam giác có thể lập được (từ 6 điểm đã cho) là:
C36 =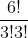
= 20 (tam giác)