Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Tham khảo a làm rồi nha: https://hoc24.vn/cau-hoi/.1904701261424
Bài 3: Xét tam giác BCD có :
BC=DC ( gt )
-> tam giác BCD cân tại C
-> ^B1 = ^D1 ( 2 góc đáy )(1)
Mặt khác : BD là tia phân giác của ^D
-> ^D1 =^D2 (2)
Từ (1) và (2) suy ra : ^B1 = ^D2 ( cùng = ^D1 )
-> BC // DA ( có cặp góc so le trong = nhau )
-> Tứ giác ABCD là hình thang ( có 2 cạnh đối song song )
Bài 4 : Từ B hạ BH vuông góc với DC (1)
Do tứ giác ABCD có ^A=^D = 900 ( gt)(2)
Từ (1) và (2) suy ra : Tứ giác ABCD là HCN ( dấu hiệu nhận biết )
-> DH = AB =2 cm ( 2 cạnh đối )
BH = AD= 2 cm ( 2 cạnh đối)
Mà DH +HC = DC= 4 (cm) ( gt)
-> HC = 2 ( cm)
Áp dụng định lí Py ta go trong tam giác vuông BHC có :
BH2 + HC2 = BC2
-> 22 + 22 = BC2
Vậy BC = \(\sqrt{8}\)(cm)
hình vẽ chỉ minh họa thôi bạn mà vẽ thì vẽ số liệu chính xác hơn nha !
Ở bài 4 có thể chứng minh tứ giác đó là hình vuông nhá bạn
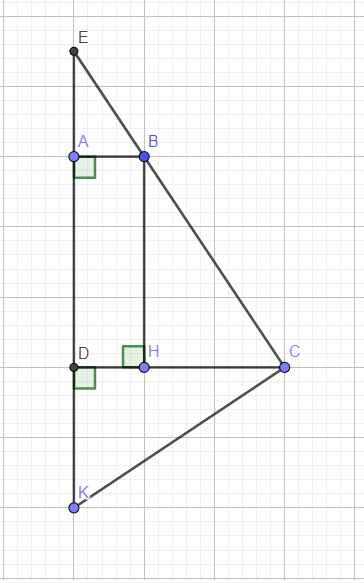
Do \(AD\perp CD\Rightarrow\) hình thang ABCD vuông tại A và D
\(\Rightarrow\) Tứ giác ABHD là hình chữ nhật (tứ giác có 3 góc vuông)
\(\Rightarrow AD=BH\) \(\Rightarrow BH=CD\)
Xét hai tam giác vuông BCH và CKD có:
\(\left\{{}\begin{matrix}BH=CD\\DK=CH\end{matrix}\right.\) \(\Rightarrow\Delta BCH=\Delta CKD\left(c.g.c\right)\) (1)
\(\Rightarrow\widehat{DCK}=\widehat{HBC}\)
\(\Rightarrow\widehat{BCK}=\widehat{BCH}+\widehat{DCK}=\widehat{BCH}+\widehat{HBC}=90^0\)
\(\Rightarrow BC\perp CK\)
b. Cũng từ (1) ta suy ra \(CB=CK\)
Áp dụng hệ thức lượng trong tam giác vuông ECK với đường cao CD:
\(\dfrac{1}{CD^2}=\dfrac{1}{CE^2}+\dfrac{1}{CK^2}=\dfrac{1}{CE^2}+\dfrac{1}{CB^2}\) (đpcm)
Gợi ý: Kẻ AH ^ CD tại H, kẻ BK ^ CD tại K
Tính được SABCD = 180cm2
từ A hạ \(AE\perp DC\)
từ B hạ \(BF\perp DC\)
\(AB//CD=>AB//EF\)\(=>ABCD\) là hình chữ nhật
\(=>AB=EF=2cm\)
vì ABCD là hình thang cân\(=>\left\{{}\begin{matrix}AD=BC\\\angle\left(ADE\right)=\angle\left(BCF\right)\end{matrix}\right.\)
mà \(\angle\left(AED\right)=\angle\left(BFC\right)=90^o\)
\(=>\Delta ADE=\Delta BFC\left(ch.cgn\right)=>DE=FC=\dfrac{DC-EF}{2}=\dfrac{6-2}{2}=2cm\)
xét \(\Delta ADE\) vuông tại E có: \(AE=\sqrt{AD^2-ED^2}=\sqrt{3^2-2^2}=\sqrt{5}cm\)
\(=>S\left(ABCD\right)=\dfrac{\left(AB+CD\right)AE}{2}=\dfrac{\left(2+6\right)\sqrt{5}}{2}=4\sqrt{5}cm^2\)
