Cho hình chóp S.ABC. Trên các đoạn thẳng SABC. Trên các đoạn thẳng SA, SB, SC lần lượt lấy ba điểm A', B', C' khác với S. Chứng minh rằng :
\(\dfrac{V_{S.A'B'C'}}{V_{S.ABC}}=\dfrac{SA'}{SA}.\dfrac{SB'}{SB}.\dfrac{SC'}{SC}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 1 2019
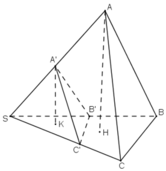
Gọi H và K lần lượt là hình chiếu vuông góc của A và A’ trên mp(SBC),
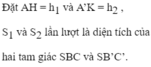
* Do A’K// AH nên bốn điểm A, A’; K và H đồng phẳng. (1)
Lại có, 3 điểm A, S, H đồng phẳng (2).
Từ (1) và (2) suy ra, 5 điểm A, A’, S. H và K đồng phẳng.
Trong mp(ASH) ta có: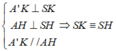 
⇒ Ba điểm S, H và K thẳng hàng.
* Ta có:
CM
8 tháng 6 2018
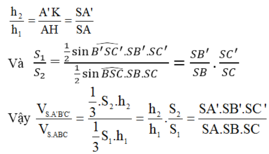
Đáp án A
Ta có
S A ' S A = 2 5 ; S B ' S B = 1 4 ; S C ' S C = 1 3 . ⇒ V S A ' B ' C ' V S A B C = 2 5 . 1 4 . 1 3 = 1 30 .
Gọi h và h’ lần lượt là chiều cao hạ từ A, A’ đến mặt phẳng (SBC).
Gọi S1 và S2 theo thứ tự là diện tích các tam giác SBC và SB’C’.
Khi đó ta có h′h=SA′SAh′h=SA′SA và 12B′SC′.SB′.SC′12BSC.SB.SC=SB′SB.SC′SC12B′SC′.SB′.SC′12BSC.SB.SC=SB′SB.SC′SC
Suy ra VS.A′B′C′VS.ABC=VA′.SB′C′VA.SBC=13h′S213hS1=SA′SA⋅SB′SB⋅SC′SCVS.A′B′C′VS.ABC=VA′.SB′C′VA.SBC=13h′S213hS1=SA′SA⋅SB′SB⋅SC′SC
Đó là điều phải chứng minh.