Trong mặt phẳng tọa độ Oxy, trên các tia Ox và Oy lần lượt lấy các điểm A và B thay đổi sao cho đường thẳng AB luôn tiếp xúc với đường tròn tâm O bán kính 1. Xác định tọa độ của A và B để đoạn AB có độ dài nhỏ nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
27 tháng 2 2019
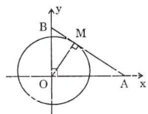
Gọi tiếp điểm của AB và đường tròn tâm O, bán kính 1 là M, ta có: OM ⊥ AB.
ΔOAB vuông tại O, có OM là đường cao nên MA.MB = MO2 = 1 (hằng số)
Áp dụng bất đẳng thức Cô-si ta có:
MA + MB ≥ 2√MA.MB = 2. √1 = 2
Dấu « = » xảy ra khi MA = MB = 1.
Khi đó OA = √(MA2 + MO2) = √2 ; OB = √(OM2 + MB2) = √2.
Mà A, B nằm trên tia Ox và Oy nên A(√2; 0); B(0; √2)
Vậy tọa độ là A(√2, 0) và B(0, √2).
20 tháng 2 2016
Ta có : HA.HB=OH²=1 (không đổi).
và AB=HA+HB ≥ 2√(HA.HB) = 2.√OH² = 2.
-> AB ≥ 2.
Vậy AB có độ dài nhỏ nhất là 2 khi HA=HB
Khi đó tg OHB và OHA vuông cân và có cạnh góc vuông = 1.
suy ra OA = OB =√2.
Vậy đoạn AB nhỏ nhất khi A(√2;0) B(0;√2).
tick cho mk nha
9 tháng 7 2021
Có \(d_{\left(O;AB\right)}=R=1\)
Áp dụng hệ thức lượng có:
\(d_{\left(O;AB\right)}.AB=OB.OA\)
\(\Leftrightarrow AB=OB.OA\)
\(\Leftrightarrow AB\le\dfrac{OB^2+OA^2}{2}=\dfrac{AB^2}{2}\)
\(\Leftrightarrow AB^2-2AB\ge0\)\(\Rightarrow AB\ge2\)
Vậy \(AB_{min}=2\) khi \(\left\{{}\begin{matrix}OA=OB\\OA.OB=2\end{matrix}\right.\)\(\Leftrightarrow a=b=\sqrt{2}\)
ML
19 tháng 1 2016
Ta có: 2SOAB = AB.OH = AB (vì OH = 1).
Vậy diện tích ∆OAB nhỏ nhất khi AB có độ dài ngắn nhất.
Vì AB = AH + HB mà AH.HB = OH2 = 1 nên AB có giá trị nhỏ nhất khi AH = HB tức ∆OAB vuông cân: OA = OB và
AB = 2AH = 2OH = 2.
AB2 = 4 = 2OA2 = 2OH = OA = OB = √2.
Khi đó tọa độ của A, B là A(√2; 0) và B(0; √2).
12 tháng 5 2023
AB tiếp xúc (O) tại H
=>OH vuông góc AB và OH=R=1
ΔOAB vuông tại O nên 1/OH^2=1/OA^2+1/OB^2
=>1/OA^2+1/OB^2=1
\(\dfrac{1}{OA^2}+\dfrac{1}{OB^2}>=\dfrac{2}{OA\cdot OB}\)
=>OA*OB>=2
=>\(S_{OAB}>=1\)
Dấu = xảy ra khi OA=OB=căn 2
AH
Akai Haruma
Giáo viên
23 tháng 5 2021
Lời giải:
Áp dụng định lý Pitago: $OA=\sqrt{1^2+1^2}=\sqrt{2}$
Vì $B\in Ox$ nên tọa độ của $B$ có dạng $(b,0)$
Vì $B$ thuộc đường tròn tâm $O$ bán kính $OA=\sqrt{2}$ nên $|x_B|=OB=OA=\sqrt{2}$. Vậy $B(\pm \sqrt{2},0)$
$C\in Oy$ nên $C$ có tọa độ $(0,c)$
$C$ thuộc đường tròn đường kính $OA$ nên:
$|y_C|=OC=OA=\sqrt{2}$. Vậy $C(0, \pm \sqrt{2})$
Ta có : HA.HB=OH²=1 (không đổi).
và AB=HA+HB ≥ 2√(HA.HB) = 2.√OH² = 2.
-> AB ≥ 2.
Vậy AB có độ dài nhỏ nhất là 2 khi HA=HB
Khi đó tg OHB và OHA vuông cân và có cạnh góc vuông = 1.
suy ra OA = OB =√2.
Vậy đoạn AB nhỏ nhất khi A(√2;0) B(0;√2).