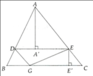
Cho tam giác ABC có đường cao AH trọng tâm G. Một đường thẳng đi qua G và song song với BC cắt các cạnh AB, AC tại M và N.
Nếu diện tích tam giác ABC bằng 36cm2 thì diện tích tam giác HMN bằng ......... cm2.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 2 2017
Ta có: MN II BC => HK\(⊥\)MN
Theo Talet có: \(\frac{HK}{AH}=\frac{GD}{AD}=\frac{1}{3}\)
và: \(\frac{MG}{BD}=\frac{AG}{AD}=\frac{2}{3}\)(*)
\(\frac{GN}{DC}=\frac{AG}{AD}=\frac{2}{3}\)(**)
tỪ (*) và (**) => \(\frac{MN}{BC}=\frac{2}{3}\)
Vậy diện tích tam giác HMN=\(S_{HMN}=\frac{2}{9}.S_{ABC}=\frac{2.36}{9}=8\)
HN
28 tháng 2 2016
mình không vẽ hình nha bạn cứ làm theo lời mình là ra
gọi AG cắt BC tại K
MN//BC=>MN/BC=AM/AB=AN/AC=AG/AK(theo định lý Ta-lét)
mà AG là trọng tâm của tam giác ABC =>AG/AK=2/3
=>MN/BC=AM/AB=AN/AC=2/3
hay MN=2BC/3
gọi AH cắt MN tại I
=>HI/AH=BM/AB=1/3
hay HI=AH/3
mà diện tích tam giác ABC bằng 36
=>1/2 AH.BC=36
<=>AH.BC=72
DIÊN TÍCH TAM GIÁC MNH LÀ
1/2 HI.MN=1/2.AH/3.2BC/3=AH/3.BC/3(mình nhân 1/2 với 2BC/3 trước đấy nha)
=(AH.BC)/3=72/3=24cm2
đáp số 24cm2
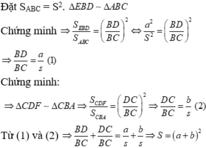
4.Bạn đặt S HNO (O giao AH với MN) là x
=> S ANO=2x
S HNC = 3x/2
Tường tự đặt BMO là y..
=> x=4