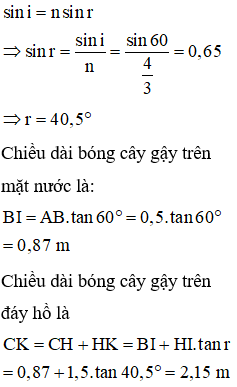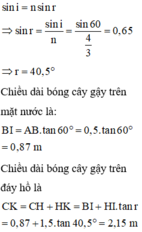Một cây gậy dài 3,5m cắm thẳng đứng ở đấy hồ gậy nhô lên khỏi mặt nước 42cm ánh sáng mặt trời chiếu xuống hồ hợp với Pháp tuyến của mặt nước một góc Pi/4 tìm chiều dài bóng của cây cây in trên đầu hồ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HD
Hà Đức Thọ
Admin
18 tháng 4 2016
Bài này không cho chiết suất của nước nên mình lấy n = 4/3
Chiều dài bóng của gậy in trên hồ là CE = CD + DE.
\(\dfrac{\sin 60^0}{\sin DIE}=\dfrac{4}{3}\Rightarrow \sin DIE = \dfrac{3\sqrt 3}{8}\) \(\Rightarrow DIE = 40^0\)
\(CE=CD+DE=BI+DE=0,5.\tan 60^0+1,5.\tan 40^0=2,12m\)
DT
16 tháng 7 2017
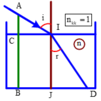
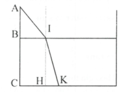
1) Hình vẽ:
a) Khi gậy đặt thẳng đứng, bóng của gậy có chiều dài:
b) Để bóng cây gậy dài nhất, gậy phải được đặt theo phương vuông góc với phương truyền sáng. Þ Góc tạo bởi cây gậy và phương ngang là 300.
Chiều dài lớn nhất của bóng: 
.
2) Hình vẽ minh họa:
Do tia phản xạ có phương nằm ngang nên 
.(so le trong) 
TH1, hình 2c: 
TH2, hình 2b: 
Từ hình vẽ: 
15 tháng 12 2018
Giải:
Chiều dài bóng của cây cọc thứ nhất gấp chiều dài của nó là:
204:156=1,5 (lần)
Vậy chiều dài bóng của cây cọc thứ hai là:
104x1,5=156(cm)
Đáp số: 156 cm.
15 tháng 12 2018
Chiều dài bóng của cây cọc thứ nhất gấp chiều dài của nó là:
204 : 156 = 1,5(lần)
Vậy chiều dài bóng của cây cọc thứ hai là:
104 x 1,5 = 156(cm)
Đáp số :156 cm
10 tháng 9 2021
Chỉ là bài giải tương tự thôi nha số liệu ko giống nha
Áp dụng định luật khúc xạ ta có:
