Tổng tất cả các nghiệm của phương trình:
là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
17 tháng 12 2019
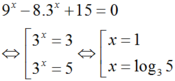
Tổng tất cả các nghiệm của phương trình là: 1 + log 3 5 = log 3 15 .
Chọn: B
PT
1

CM
13 tháng 3 2019
Đáp án D
Phương trình

Vậy tổng các nghiệm của phương trình đã cho trên đoạn 0 ; 4 π là 8 π
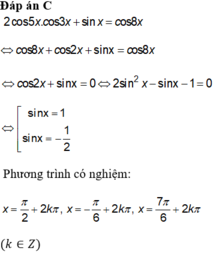





Đặt: \(x+\dfrac{1}{x}=t\)
\(x^2+\dfrac{1}{x^2}=t^2-2\) \(\)
Ta có: \(18\left(x+\dfrac{1}{x}\right)^2+9\left(x^2+\dfrac{1}{x^2}\right)^2-9\left(x^2+\dfrac{1}{x^2}\right)\left(x+\dfrac{1}{x}\right)^2=\left(x+2\right)^2\)
\(\Leftrightarrow\) \(18t^2+9\left(t^2-2\right)^2-9t^2\left(t^2-2\right)=\left(x+2\right)^2\)
\(\Leftrightarrow\) \(18t^2+9t^4-36t^2+36-9t^4+18t^2=\left(x+2\right)^2\)
\(\Leftrightarrow\) \(\left(x+2\right)^2=36\)
\(\Leftrightarrow\) \(\left[{}\begin{matrix}x+2=6\\x+2=-6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-8\end{matrix}\right.\)
Vậy: Tổng tất cả các nghiệm của phương trình: \(18\left(x+\dfrac{1}{x}\right)^2+9\left(x^2+\dfrac{1}{x^2}\right)^2-9\left(x^2+\dfrac{1}{x^2}\right)\left(x+\dfrac{1}{x}\right)^2=\left(x+2\right)^2\) là \(-8+4=-4\) .
18(x+\(\dfrac{1}{x}\))2+9(x2+\(\dfrac{1}{x^2}\))2-9(x2+\(\dfrac{1}{x^2}\))(x+\(\dfrac{1}{x}\))2=(x+2)2
Đặt (x+\(\dfrac{1}{x}\))2=t (t>0)\(\Rightarrow x^2+\dfrac{1}{x^2}=t-2\)
Khi đó vế phải của phương trình trở thành:
18t2+9(t-2)2-9t(t-2)=36
\(\Rightarrow\left(x+2\right)^2=36\)
\(\Rightarrow\left[{}\begin{matrix}x=4\\x=-8\end{matrix}\right.\)
Vậy tổng các nghiệm của phương trình là:4+(-8)=-4