Dựa trên hàm số y=sin x, học sinh xây dựng kiến thức hàm số y=cos x
Mn giúp mình với ạ. Mình đang cần gấp ạ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BG
1
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 10 2021
\(y=\dfrac{2x-1}{x+m}\Rightarrow y'=\dfrac{2m+1}{\left(x+m\right)^2}\)
Hàm nghịch biến trên miền xác định khi:
\(2m+1< 0\Rightarrow m< -\dfrac{1}{2}\)
RH
7 tháng 1 2022
b) f(1) + 2f(-2) = a - 1 + 2(a - 1).(-2) = a - 1 - 4a + 4 = -3a + 3 = -3(a - 1) = f(-3) (đpcm)
N
26 tháng 1 2020
Bạn nào biết giải thì comment nhanh lên ạ . Ai comment nhanh nhất thì mình sẽ k cho ( nhưng phải hợp lý một chút ạ )
5 tháng 3 2020
Tính độ dài OM dùng định lý Pytago : \(OM^2=3^2+1^2\)
Từ đó tính ra OM. Mình làm sai à?
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
30 tháng 12 2022
a, với m = 1 thay m = 1 vào hàm số : y = ( 3-2m)x+ m-1 ta có :
y = ( 3-2.1)x+1-1
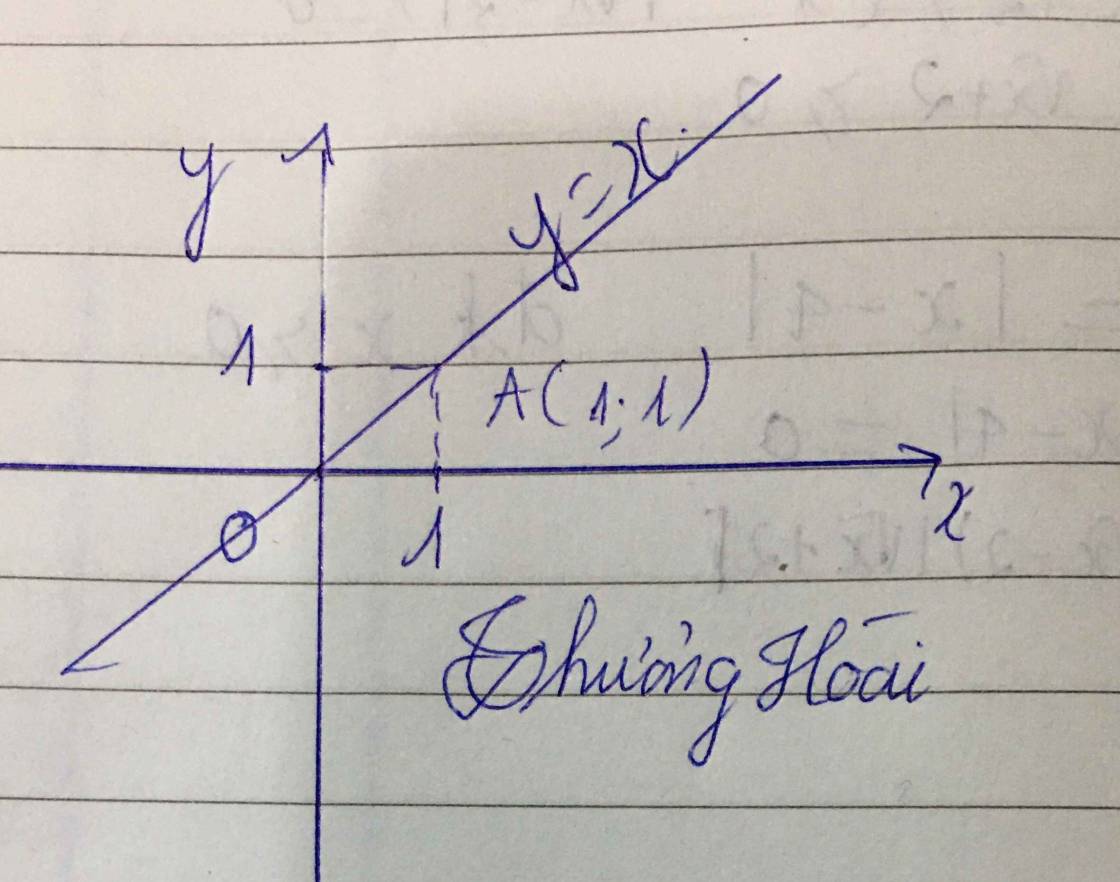
y = x
Đồ thị hàm số giao với trục Ox tại điểm có tung độ bằng 0 nên; y =0
=> x = 0
Đồ thị hàm số đi qua điểm O(0;0)
với x = 1 => y = 1 .
Đồ thị đi qua A(1;1)
b, Gọi B (x1;y1) là giao điểm của hàm số y= (3-2m)x + m-1và hàm số
2x-3 = 0 .
Theo bài ra ta có: y1 = 0 => (3-2m)x1 + m - 1 = 0
Vì B là giao điểm của hai đt nên tọa độ điểm B thỏa mãn hàm số :
2x - 3 = 0=> 2x1 - 3 = 0 => x1 = 3/2
Thay x1 = 3/2 vào pt (3-2m)x1 +m -1 = 0 ta có :
(3-2m) .3/2 + m - 1 = 0
9/2 - 3m + m - 1 = 0
-2m + 7/2 = 0
m = 7/4
Kết luận với m = 7/4 thì đồ thị hàm số : y =( 3-2m)x+m-1
có dạng : y = -1/2x + 3/4 và giao với đồ thị 2x-3 = 0 tại điểm B( 3/2; 0)
và điểm B nằm trục hoành
NT
0
AH
Akai Haruma
Giáo viên
27 tháng 8 2021
Lời giải:
a. Để hàm trên là hàm bậc nhất thì $\frac{m-2}{m+3}\neq 0$
\(\Leftrightarrow \left\{\begin{matrix} m-2\neq 0\\ m+3\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m\neq 2\\ m\neq -3\end{matrix}\right.\)
b. Để hàm trên đồng biến thì $\frac{m-2}{m+3}>0$
\(\Leftrightarrow \left[\begin{matrix} \left\{\begin{matrix} m-2>0\\ m+3>0\end{matrix}\right.\\ \left\{\begin{matrix} m-2<0\\ m+3< 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} m>2\\ m< -3\end{matrix}\right.\)
Để hàm trên nghịch biến thì $\frac{m-2}{m+3}< 0$
\(\Leftrightarrow \left[\begin{matrix} \left\{\begin{matrix} m-2>0\\ m+3< 0\end{matrix}\right.\\ \left\{\begin{matrix} m-2< 0\\ m+3>0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} -3> m>2(\text{vô lý}\\ -3< m< 2\end{matrix}\right.\Leftrightarrow -3< m< 2\)