Tìm nghiệm của phương trình 2x6+y2+2x3y=64
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì tỉ số giữa hai nghiệm khác 1 nên pt có hai nghiệm pb
\(\Rightarrow\Delta=4m^2-4\left(2m-1\right)>0\)
\(\Leftrightarrow m\ne1\)
Áp dụng viet có: \(\left\{{}\begin{matrix}y_1+y_2=2m\\y_1y_2=2m-1\end{matrix}\right.\)
Giả sử \(y_1=2y_2\)
Có hệ: \(\left\{{}\begin{matrix}y_1+y_2=2m\\y_1=2y_2\\y_1y_2=2m-1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y_1=\dfrac{4m}{3}\\y_2=\dfrac{2m}{3}\\y_1y_2=2m-1\end{matrix}\right.\)\(\Rightarrow\dfrac{4m}{3}.\dfrac{2m}{3}=2m-1\)
\(\Leftrightarrow8m^2-18m+9=0\) \(\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{3}{2}\\m=\dfrac{3}{4}\end{matrix}\right.\)(tm)

Ta có x4 + x2 + 1 = y2
Lại có x4 + 2x2 + 1 ≥ x4 + x2 + 1 hay (x2 + 1)2 ≥ x4 + x2 + 1
=> (x2 + 1)2 ≥ y2 (1)
Lại có x4 + x2 + 1 > x4 => y2 > x4 (2)
Từ (1) và (2), ta có x4 < y2 ≤ (x2 + 1)2
<=> y2 = (x2 + 1)2 = x4 + 2x2 + 1
Mà x4 + x2 + 1 = y2 => x4 + 2x2 + 1 = x4 + x2 + 1
<=> x2 = 0 <=> x = 0
Thay vào, ta có 1 = y2 <=> y ∈ {-1,1}
Vậy ...

Lời giải:
Hiển nhiên $x\geq 0$
Ta có: $2^x=y^2-57\equiv y^2\equiv 0,1\pmod 3$
$\Leftrightarrow (-1)^x\equiv 0,1\pmod 3$
$\Rightarrow x$ chẵn.
Đặt $x=2a$ với $a$ là số tự nhiên.
Khi đó: $2^{2a}-y^2=-57$
$\Leftrightarrow (2^a-y)(2^a+y)=-57$
Đến đây là dạng phương trình tích cực kỳ đơn giản nên bạn có thể tự xét TH để giải. Kết quả $a=3; y=11$ hay $x=6; y=7$
Lời giải:
Hiển nhiên $x\geq 0$
Ta có: $2^x=y^2-57\equiv y^2\equiv 0,1\pmod 3$
$\Leftrightarrow (-1)^x\equiv 0,1\pmod 3$
$\Rightarrow x$ chẵn.
Đặt $x=2a$ với $a$ là số tự nhiên.
Khi đó: $2^{2a}-y^2=-57$
$\Leftrightarrow (2^a-y)(2^a+y)=-57$
Đến đây là dạng phương trình tích cực kỳ đơn giản nên bạn có thể tự xét TH để giải. Kết quả $a=3; y=11$ hay $x=6; y=7$

<=>x^2+y^2-x-y-xy=0
<=>2x^2+2y^2-2x-2y-2xy=0
<=>(x-y)^2+(x-1)^2+(y-1)^2=2
mà 2=0+1+1=1+0+1=1+1+0
(phần này tách số 2 ra thành tổng 3 số chính phương)
Xét trường hợp 1:
(x-y)^2=0
(x-1)^2=1
(y-1)^2=1
Giải ra ta được x=2, y=2
Tương tự xét các trường hợp còn lại.
Kết quả: 5 nghiệm: (2;2) ; (1;0) ; (1;2) ; (0;1) ; (2;1)
x2 - xy + y2 = x - y
<=> x2 - xy + y2 - x + y = 0
<=> x ( x - y) + y2 - ( x - y) = 0
<=> (x-1)(x-y)y2 =0

Ta có
x + 1 4 − y 2 = x + y + 1 x − 2 2 + y − 1 3 = x + y − 1
⇔ x + 1 − 2 y = 4 x + 4 y + 4 3 x − 6 + 2 y − 2 = 6 x + 6 y − 6
⇔ 3 x + 6 y = − 3 3 x + 4 y = − 2 ⇔ y = − 1 2 x = 0
Thay x = 0; y = − 1 2 vào phương trình (m + 2)x + 7my = m – 225 ta được:
(m + 2).0 + 7m − 1 2 = m – 225 ⇔ 9 2 m = 225 ⇔ m = 50
Đáp án: C

Điều kiện x ≥ − 7 y ≥ − 1 3 *
x 2 + 2 x y + 8 x = 3 y 2 + 12 y + 9 ( 1 ) x 2 + 4 y + 18 − 6 x + 7 − 2 x 3 y + 1 = 0 ( 2 )
Có 1 ⇔ x 2 + 2 y + 4 x − 3 y 2 − 12 y − 9 = 0 , ta coi (1) là phương trình bậc hai ẩn x và y là tham số, giải x theo y ta được x = − 3 y − 9 x = y + 1
Với x = − 3 y − 9 thì (*) ⇒ − 3 y − 9 ≥ − 7 y ≥ − 1 3 ⇔ y ≤ − 2 3 y ≥ − 1 3 (vô lí)
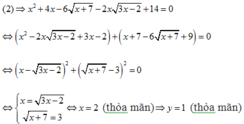
Hệ phương trình có nghiệm là 2 ; 1 ⇒ a = 2 , b = 1 ⇒ T = 24
Đáp án cần chọn là: A


\(x^5\) - 2\(x^4\) - (y2 + 3)\(x\) + 2y2 - 2 = 0
(\(x^5\) - 2\(x^4\))- (y2 + 3)\(x\) + 2.(y2 + 3) - 8 = 0
\(x^4\).(\(x\) - 2) - (y2 + 3).(\(x\) - 2) - 8 = 0
(\(x\) - 2).(\(x^4\) - y2 - 3) = 8
8 = 23; Ư(8) = {-8; - 4; -2; - 1; 1; 2; 4; 8}
Lập bảng ta có:
| \(x-2\) | -8 | -4 | -2 | -1 | 1 | 2 | 4 | 8 |
| \(x\) | -6 | -2 | 0 | 1 | 3 | 4 | 6 | 10 |
| \(x^4\) - y2 - 3 | -1 | -2 | -4 | -8 | 8 | 4 | 2 | 1 |
| y | \(\pm\)\(\sqrt{1294}\) | \(\pm\)\(15\) | \(\pm\)1 | \(\pm\)\(\sqrt{6}\) | y2 = -10 (ktm) | \(\pm\)\(\sqrt{249}\) | \(\pm\)\(\sqrt{1291}\) | \(\pm\)\(\sqrt{9996}\) |
vì \(x\); y nguyên nên theo bảng trên ta có các cặp \(x\); y thỏa mãn đề bài là:
(\(x\); y) = (0; -1;); (0; 1)
nghiệm nguyên
<=> y2 + 2x3y + 2x6 - 64 = 0 (1)
Coi (1) là phương trình bậc 2 ẩn y, x là tham số
(1) có nghiệm <=> Δ ≥ 0 <=> ( 2x3 )2 - 4( 1 + 2x6 - 64 ) ≥ 0
<=> 4x6 - 4 - 8x6 + 256 ≥ 0 <=> -4x6 + 252 ≥ 0 <=> x ∈ { -1 ; 0 ; 1 } ( giải bpt này khó v nên cho nghiệm luôn )
+) Với x = -1 (1) trở thành y2 - 2y - 62 = 0 có Δ = 252 không là SCP nên không có nghiệm nguyên
+) Với x = 0 (1) trở thành y2 - 64 = 0 <=> y = ±8 (tm)
+) Với x = 1 (1) trở thành y2 + 2y - 62 = 0 có Δ = 252 không là SCP nên không có nghiệm nguyên
Vậy ( x ; y ) ∈ { ( 0 ; 8 ) , ( 0 ; -8 ) }