Giúp em với ạ. Em cần gấp lắm ạ. Em cảm ơn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TL
1
Những câu hỏi liên quan
giúp em với ạ em đang cần gấp lắm ạ em cảm ơn trước
TM
3 tháng 7 2023
(a) \(A=\dfrac{3}{x-2}\in Z\)
\(\Rightarrow\left(x-2\right)\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)
\(\Rightarrow\left[{}\begin{matrix}x-1=1\\x-1=-1\\x-1=3\\x-1=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=0\\x=4\\x=-2\end{matrix}\right.\)
Vậy: \(x\in\left\{-2;0;2;4\right\}.\)
(b) \(B=-\dfrac{11}{2x-3}\in Z\)
\(\Rightarrow\left(2x-3\right)\inƯ\left(11\right)=\left\{\pm1;\pm3\right\}\)
\(\Rightarrow\left[{}\begin{matrix}2x-3=1\\2x-3=-1\\2x-3=11\\2x-3=-11\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=1\\x=7\\x=-4\end{matrix}\right.\)
Vậy: \(x\in\left\{-4;1;2;7\right\}.\)
(c) \(C=\dfrac{x+3}{x+1}=\dfrac{\left(x+1\right)+2}{x+1}=1+\dfrac{2}{x+1}\in Z\Rightarrow\dfrac{2}{x+1}\in Z\)
\(\Rightarrow\left(x+1\right)\inƯ\left(2\right)=\left\{\pm1;\pm2\right\}\)
\(\Rightarrow\left[{}\begin{matrix}x+1=1\\x+1=-1\\x+1=2\\x+1=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\\x=1\\x=-3\end{matrix}\right.\)
Vậy: \(x\in\left\{-3;-2;0;1\right\}.\)
(d) \(D=\dfrac{2x+10}{x+3}=\dfrac{2\left(x+3\right)+4}{x+3}=2+\dfrac{4}{x+3}\in Z\Rightarrow\dfrac{4}{x+3}\in Z\)
\(\Rightarrow\left(x+3\right)\inƯ\left(4\right)=\left\{\pm1;\pm2\pm4\right\}\)
\(\Rightarrow x\in\left\{-2;-4;-1;-5;1;-7\right\}\)
HK
1
10 tháng 12 2021
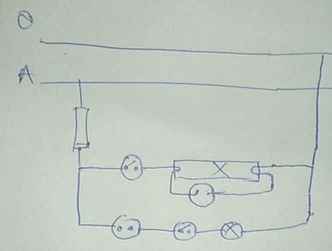
Câu 1.
Khi mở khóa K:
\(I_m=I_1=0,4A\)
Khi đóng khóa K:
\(I_m=I_1+I_2=0,6\Rightarrow I_2=0,2A\)
\(U_1=0,4\cdot5=2V\)
\(\Rightarrow U_2=U_1=2V\)
\(\Rightarrow U=U_1=U_2=2V\)
\(R_2=\dfrac{U_2}{I_2}=\dfrac{2}{0,2}=10\Omega\)
HN
0
H7
2
MB
3
17 tháng 9 2021
Gọi tam giác ABC vuông tại A, trung tuyến AM, đường cao AH
\(\Rightarrow AM=5\left(cm\right);AH=4\left(cm\right)\)
Ta có AM là trung tuyến ứng với cạnh huyền BC
\(\Rightarrow BC=2AM=10\left(cm\right)\)
Áp dụng HTL tam giác \(AH\cdot BC=AB\cdot AC\Rightarrow AB\cdot AC=40\Rightarrow AB=\dfrac{40}{AC}\\ \dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\\ \Rightarrow\dfrac{1}{16}=\dfrac{1}{\dfrac{1600}{AC^2}}+\dfrac{1}{AC^2}\\ \Rightarrow\dfrac{AC^4+1600}{1600AC^2}=\dfrac{100AC^2}{1600AC^2}\Rightarrow AC^4-100AC^2+1600=0\\ \Rightarrow\left(AC^2-80\right)\left(AC^2-20\right)=0\\ \Rightarrow\left[{}\begin{matrix}AC^2=80\\AC^2=20\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}AC=4\sqrt{5}\left(AC>0\right)\\AC=2\sqrt{5}\left(AC>0\right)\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}AB=2\sqrt{5}\\AB=4\sqrt{5}\end{matrix}\right.\)
Vậy với AB là cạnh góc vuông lớn thì \(\left(AB;AC;BC\right)=\left(4\sqrt{5};2\sqrt{5};10\right)\)
TD
2
Q
19 tháng 5 2021
vẽ lại mạch ta có RAM//RMN//RNB
đặt theo thứ tự 3 R là a,b,c
ta có a+b+c=1 (1)
điện trở tương đương \(\dfrac{1}{R_{td}}=\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\) \(\Rightarrow I=\dfrac{U}{R_{td}}=9.\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\) với a,b,c>0
áp dụng bất đẳng thức cô si cho \(\dfrac{1}{a},\dfrac{1}{b},\dfrac{1}{c}\) \(\Rightarrow\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\ge\dfrac{3}{\sqrt[3]{abc}}\ge\dfrac{3}{\left(\dfrac{a+b+c}{3}\right)}=\dfrac{9}{a+b+c}=9\)
\(\Leftrightarrow9\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\ge81\Leftrightarrow I\ge81\) I min =81 ( úi dồi ôi O_o hơi to mà vẫn đúng đá nhỉ)
dấu ''='' xảy ra \(\Leftrightarrow a=b=c\left(2\right)\)
từ (1) (2) \(\Rightarrow a=b=c=\dfrac{1}{3}\left(\Omega\right)\)
vậy ... (V LUN MẤT CẢ BUỔI TỐI R BÀI KHÓ QUÁ EM ĐANG ÔN HSG À )
1 am going to send
2 will get
3 will do
4 will be
5 are going to visit
6 will win
7 am going to take
8 are going
9 will go
10 is going to defeat
11 is going to have
12 will never lie
13 will fly
14 won't tell
15 will like