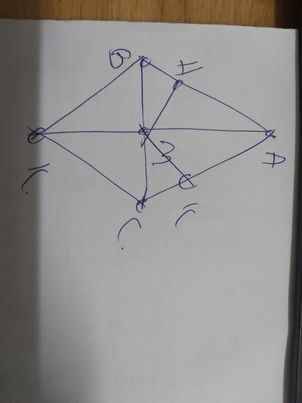
Cho tam giác ABC vuông tại A , M là trung điểm của BC . Kẻ MH vuông góc với AB (H thuộc AB).Trên tia đối của tia MH lấy điểm K sao cho MH=MK. Chứng minh rằng : a,tam giác BMH= tam giác CMK b,CK song song với AB c,Gọi D là 1 điểm thuộc tia đối của tia MA sao cho MÀ=MĐ . Chứng minh 3 điểm D,K,C thẳng hàng ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

14 tháng 1
a:
| GT | ΔABC cân tại A M là trung điểm của BC MK=MA MH\(\perp\)AB; MK\(\perp\)AC H\(\in\)AB; K\(\in\)AC |
| KL | b: ΔABM=ΔACM c: ΔABM=ΔKCM d: AB//CK e: MH=MK |
b: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
c: Xét ΔMAB và ΔMKC có
MA=MK
\(\widehat{AMB}=\widehat{KMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔMAB=ΔMKC
d: Ta có: ΔMAB=ΔMKC
=>\(\widehat{MAB}=\widehat{MKC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//KC
e: ΔAMB=ΔAMC
=>\(\widehat{MAB}=\widehat{MAC}\)
Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
\(\widehat{HAM}=\widehat{KAM}\)
Do đó: ΔAHM=ΔAKM
=>MH=MK
=>ΔMHK cân tại M
a/ Xét t/g BMH và t/g CMK có:
BM = CM (gt)
\(\widehat{BMH}=\widehat{CMK}\) (đối đỉnh)
MH = MK (gt)
=> t/g BMH = t/g CMK (c.g.c)(đpcm)
b/ Vì t/g BMH = t/g CMK (ý a)
=> \(\widehat{MBH}=\widehat{KCM}\) (2 góc tương ứng)
mà 2 góc này ở vị trí so le trong nên:
=> CK // AB (đpcm)
c/ Xét t/g ABM và t/g DCM có:
MA = MD (gt)
\(\widehat{AMB}=\widehat{DMC}\) (đối đỉnh)
BM = CM (gt)
=> t/g ABM = t/g DCM (c.g.c)
=> \(\widehat{BAM}=\widehat{CDM}\) (2 góc tương ứng)
mà 2 góc này ở vị trí so le trong nên:
=> AB // DC
Ta lại có: CK // AB (ý b)
mà DC // AB (cmt)
=> CK trùng DC
=> 3 điểm D, K, C thẳng hàng(đpcm)
Pn giỏi wá!!!!