Question

[Ngoc Ngan]

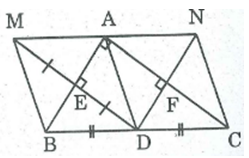
Cho tam giác ABC vuông tại A , điểm D là trung điểm của BC . Gọi M là điểm đối xứng với D qua AB , E là giao điểm của DM và AB

a) Tứ giác AEDC là hình gì ? vì sao?

b) Tứ giác ADBM la hình gì? vì sao?

c) Tam giác ABC có điều kiện gì thì tứ giác ADBM là hình vuông ?

Answer 1

[Nguyen Thi Trinh]

Vì M đối xứng với D qua AB(gt), E là giao điểm của DM và AB

\(\Rightarrow\left\{\begin{matrix}DE=ME\\DE\perp AB\end{matrix}\right.\)

Ta có: DE\(\perp\)AB(cmt), AC\(\perp\)AB( vì \(\Delta\)ABC vuông tại A)

\(\Rightarrow DE\)//AC

Xét tứ giác AEDC có DE//AC(cmt), \(\widehat{EAC}=90^0\)

\(\Rightarrow AEDC\) là hình thang vuông

Xét \(\Delta ABC\) có: D là trung điểm của BC(gt)

DE//AC(cmt)

\(\Rightarrow\) AE=BE(Trong một tam giác, đường thẳng đi qua trung điểm một cạnh và song song với cạnh thứ hai thì đi qua trung điểm cạnh còn lại)

Xét tứ giác ADBM có: DE=ME(cmt), AE=BE(cmt)

\(\Rightarrow\)ADBM là hình bình hành

Mà hình bình hành ADBM có: DE\(\perp\)AB(cmt)

\(\Rightarrow\) ADBM là hình thoi

Tứ giác ADBM là hình vuông khi tam giác ABC là tam giác vuông cân

Answer 2

[Dinh Thi Hai Ha]

a) Ta có: \(\left\{{}\begin{matrix}ED\perp AB\left(gt\right)\\AC\perp AB\left(gt\right)\end{matrix}\right.\)

=> ED // AC

Xét tứ giác EDCA có :

ED // AC (cmt)

=> EDAC là hình thang

có \(\widehat{DEA}=90^0\)

=> EDAC là hình thang cân.

b) Xét \(\Delta ABC\) có:

D là trung điểm của của Bc (gt)

ED // AC ( EDCA là hình thang vuông)

=> E là trung điểm của AB.

Xét tứ giác MBDA có:

E là trung điểm của AB (cmt)

E là trung điểm của MD ( M đối xứng D qua E)

=> MBDA là hình bình hành

có BA \(\perp\) MD

=> MBDA là hình thoi.

c) Để tứ giác MBDA là hình vuông

thì \(\widehat{BDA}=90^0\)

Để \(\widehat{BDA}=90^0\) thì

AD \(\perp\) BC

=> AD là đường cao của \(\Delta ABC\)

=> \(\Delta ABC\) phải là tam giác vuông cân ( vuông cân tại A)

chúc bạn học tốt