Cho tam giác ABC cân , có góc A= 60o các đường phân giác BD và CE cắt nhau tại I
Chứng minh ID=IE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CH
Cô Hoàng Huyền
Admin
VIP
10 tháng 1 2018
Câu hỏi của giang ho dai ca - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo tại link trên nhé.
VN
Cho tam giác ABC có góc A là 60độ. Hai tia phân giác trong BD và CE cắt nhau tại I. Chứng minh ID=IE
1
DD
Đoàn Đức Hà
Giáo viên
6 tháng 7 2021
\(\widehat{A}=60^o\Rightarrow\widehat{B}+\widehat{C}=120^o\Rightarrow\widehat{IBC}+\widehat{ICB}=60^o\Rightarrow\widehat{BIC}=120^o\)
\(\Rightarrow\widehat{BIE}=\widehat{CID}=60^o\).
Kẻ phân giác \(IF\)của \(\widehat{BIC}\).
Khi đó \(\widehat{BIF}=\widehat{CIF}=60^o\).
\(\Delta BIE=\Delta BIF\left(g.c.g\right)\Rightarrow IE=IF\)
\(\Delta CID=\Delta CIF\left(g.c.g\right)\Rightarrow ID=IF\)
Suy ra \(ID=IE\).
CM
19 tháng 11 2018
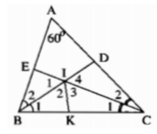
Trong ΔABC, ta có:
∠A +∠B +∠C = 180o (tổng ba góc trong tam giác)
⇒∠B +∠C = 180 - ∠A = 180 - 60 = 120o
+) Vì BD là tia phân giác của ABC nên: ∠(B1 ) = ∠(B2) = 1/2 ∠B
Vì CE là tia phân giác của góc ACB nên: ∠(C1 ) = ∠(C2) = 1/2 ∠ C
Do đó:
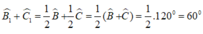
Trong ΔBIC, ta có:
∠(BIC) = 180o(∠(B1 ) + ∠(C1) = 180o - 60o = 120o
Kẻ tia phân giác ∠(BIC) cắt cạnh BC tại K
Suy ra: ∠(I2 ) = ∠(I3 ) = 1/2 ∠(BIC) = 60o
Ta có: ∠(I1 ) + ∠(BIC) = 180o (hai góc kề bù)
⇒ ∠(I1 ) = 180o-∠(BIC) = 180o - 120o = 60o
∠(I4 ) = ∠(I1) = 60o(vì hai góc đối đỉnh)
Xét ΔBIE và ΔBIK, ta có
∠(B2) = ∠(B1) (vì BD là tia phân giác của góc ABC)
BI cạnhchung
∠(I1) = ∠(I2) = 60o
Suy ra: ΔBIE = ΔBIK(g.c.g)
IK = IE (hai cạnh tương ứng) (1)
Xét ΔCIK và ΔCID, ta có
∠(C1) = ∠(C2) ( vì CE là tia phân giác của góc ACB).
CI cạnh chung
∠(I3) = ∠(I4) = 60o
Suy ra: ΔCIK = ΔCID(g.c.g)
IK = ID (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: IE = ID
5 tháng 11 2016
Xét \(\Delta BIC\)có I+B2+C2=\(^{180^0}\)
=>B2+C2=180-I
=>B2+C2=60\(^0\)
Ta lại có \(B1=B2=\frac{B}{2}\)
\(C1=C2=\frac{C}{2}\)
Mà B=C( tam giác ABC cân )
=>\(B2=C2;C1=B1\)
\(\Leftrightarrow B1+B2+C1+C2=C+B\)
\(\Leftrightarrow C+B=2\cdot B2+2\cdot C2\)
\(\Leftrightarrow C+B=120^O\)
Xét \(\Delta ABC\)có A+B+C=180O
=>A=1800-B-C
=>A=600
b)\(Xét\Delta BEI\)VÀ\(\Delta CDI\)CÓ:
B2=C2(cmt)
EIB=DIC(2 góc đối đỉnh)
BI=CI(TAM GIÁC BIC CÂN)
=>\(\Delta BIE=\Delta CID\left(c-g-c\right)\)
=>IE=ID(2 cạnh tương ứng)
Xét ΔIDE có \(\widehat{IDE}=\widehat{IED}\)
nên ΔIDE cân tại I
hay ID=IE