(1000-13)*(1000-23)*(1000-33)..........(1000-503)=.............
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Ta có : 1+13+25+37+...+99/1000
Ta tính tử số
Số số hạng của tử số là : (99-1)/12+1
Sai đề bạn ơi

khanh rat de doc ki de roi neu ko hieu thi nhan tin hoi minh
Viết đầy đủ các số hạng ta có:
1/1000 + 13/1000 + 25/1000 + 37/1000 + 49/1000 + 51/1000 + 63/1000 + 75/1000 + 87/1000 + 99/1000
= 1 + 13 + 25 + 37 + 49 + 51 + 63 + 75 + 87 + 99/ 1000
= ( 1 + 99 ) + ( 13 + 87) + ( 25 + 75 ) + ( 37 + 63) + ( ( 49 + 51)/ 1000
= 5 x 100/ 1000
= 500/ 1000
= 1/2

\(\frac{1}{1000}+\frac{13}{1000}+\frac{25}{1000}+....+\frac{109}{1000}\)
\(=\frac{1+13+25+....+109}{1000}\)
Áp dụng công thức tính dãy số ta có
\(1+13+25+...+109=\frac{\left[\left(109-1\right):12+1\right].\left(109+1\right)}{2}=\frac{10.110}{2}=10.55=550\)
Vậy
\(\frac{1+13+25+...+109}{1000}=\frac{550}{1000}=\frac{11}{20}\)
\(\frac{1}{1000}+\frac{13}{1000}+\frac{25}{1000}+.......+\frac{109}{1000}\)
\(\frac{1+13+25+37+.....+97+109}{1000}\)
\(\frac{\left(\left(109-1\right):12+1\right).\left(109+1\right):2}{1000}\)
\(\frac{550}{1000}\)
= \(\frac{11}{20}\)



M =1/1000+13/1000+25/1000+37/1000+...+121/1000+133/1000
\(M=\frac{1+13+25+...+133}{1000}\)
\(M=\frac{\left(133+1\right)\times12:2}{1000}\)
\(M=\frac{804}{1000}=0,804\)

{1/1000+49/1000} + {13/1000+37/1000}+25/1000=50/1000+50/1000+25/1000
=125/1000
nhớ cho nhé!kb lun
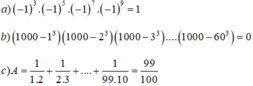
\(\left(1000-1^3\right)\left(1000-2^3\right)\left(1000-3^3\right)....\left(1000-50^3\right)\)
\(=\left(10^3-1^3\right)\left(10^3-2^3\right)\left(10^3-3^3\right)....\left(10^3-10^3\right)....\left(10^3-50^3\right)\)
\(=\left(10^3-1^3\right)\left(10^3-2^3\right)\left(10^3-3^3\right)....0....\left(10^3-50^3\right)\)
=0
\(\left(1000-1^3\right).\left(1000-2^3\right).\left(1000-3^3\right).....\left(1000-50^3\right)\)
\(=\left(1000-1^3\right).\left(1000-2^3\right).\left(1000-3^3\right).\left(1000-4^3\right).....\left(1000-9^3\right).\left(1000-10^3\right).....\left(1000-50^3\right)\)\(=\left(1000-1^3\right).\left(1000-2^3\right).\left(1000-3^3\right).\left(1000-4^3\right).....\left(1000-9^3\right).\left(1000-1000\right).....\left(1000-50^3\right)\)
\(=\left(1000-1^3\right).\left(1000-2^3\right).\left(1000-3^3\right).\left(1000-4^3\right).....\left(1000-9^3\right).0.....\left(1000-50^3\right)\)\(=0\)