Cho tam giác ABC cân tại A. Trên tia đối của BA, lấy D, Trên tia CA, lấy E sao cho BD=CE. Gọi M là giao điểm của BC và DE. Vẽ EF song song với BC ( F thuộc AB )
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
16 tháng 2 2019
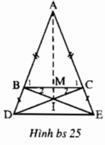
Các tam giác cân ABC và ADC có chung góc ở đỉnh ∠A nên ∠B1 = ∠ADE. Mà hai góc này ở vị trí đồng vị nên suy ra BC // DE.
LC
31 tháng 3 2017
“““““` ✬ ‘✧ ‘✬
““““` __♜_♜_♜__
“““` `{,,,,,,,,,,,,,,,,,,,,,}
‘“` ✩`{✫//✰//✰//✫}` ✩
‘“` ♖_{♖___♖__♖___.♖}_♖
“` {///////////////}
“`{,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,}
“{//////////////////}
“{_✿__❀_♥_✿_♥_❀__✿_}
““““ * ` ` * ` ` *
‘““““ 0 ` ` 0 ` ` 0
““““ ||___||___||
““ * ` {,,,,,,,,,,,,,,,,,,,} ` *
““ 0 ` {////////} ` 0
‘“`_||_{_______”_____}_||_
“`{///////////////}
“`{,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,}
“`{///////////////}
“`{_____________”________}
CH
Cô Hoàng Huyền
Admin
VIP
15 tháng 6 2016
Bài này ta chủ yếu chứng minh các tam giác bằng nhau.
a. Xét tam giác BDF cân do có : góc DBF = ACB(Tam giác ABC cân) = DFB (Đồng vị)
b. Xét tam giác FMD và tam giác CME có:
Góc FDM =góc MEC(so le trong)
góc DFM = góc MCE (So le trong)
DF = CE(=DB)
\(\Rightarrow\Delta FMD=\Delta CME\left(g-c-g\right)\Rightarrow MD=ME\) (Hai cạnh tương ứng)
c. Ta có \(\Delta DCM=\Delta EFM\left(c-g-c\right)\Rightarrow DC=EF\)