Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
Do đó: AEHF là hình chữ nhật
xin lỗi anh(chị) em mới lớp 6 không giải đc
thật lòng xin lỗi :(((((
((((((((🙄)))))))))___________bn ghi như mình đi thì bn sẽ có cái nịt 👉👈!!!
a: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
Do đó: AEHF là hình chữ nhật
a: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
Do đó: AEHF là hình chữ nhật
b: Xét tứ giác DHEF có
HE//DF
HE=DF
Do đó: DHEF là hình bình hành
a: Xét tứ giác AEHF có
góc AEH=góc AFH=góc FAE=90 độ
=>AEHF là hình chữ nhật
b: FA=FD
FA=HE
=>HE=FD
Xét tứ giác HEFD có
HE//FD
HE=FD
=>HEFD là hình bình hành
c: Sửa đề: MP vuông góc AB
M đối xứng G qua AB
=>MG vuông góc AB tại trung điểm của MG
=>MG vuông góc AB tại P và P là trung điểm của MG
XétΔABC có
M là trung điểm của BC
MP//AC
=>P là trung điểm của AB
Xét tứ giác AMBG có
P là trung điểm chung của AB và MG
MA=MB
=>AMBG là hình thoi
M đối xứng K qua AC
=>MK vuông góc AC tại trung điểm của MK
=>Q là trung điểm của MK
Xét ΔABC có
M là trung điểm của BC
MQ//AB
=>Q là trung điểm của AC
Xét tứ giác AMCK có
Q là trung điểm chung của AC và MK
MA=MC
=>AMCK là hình thoi
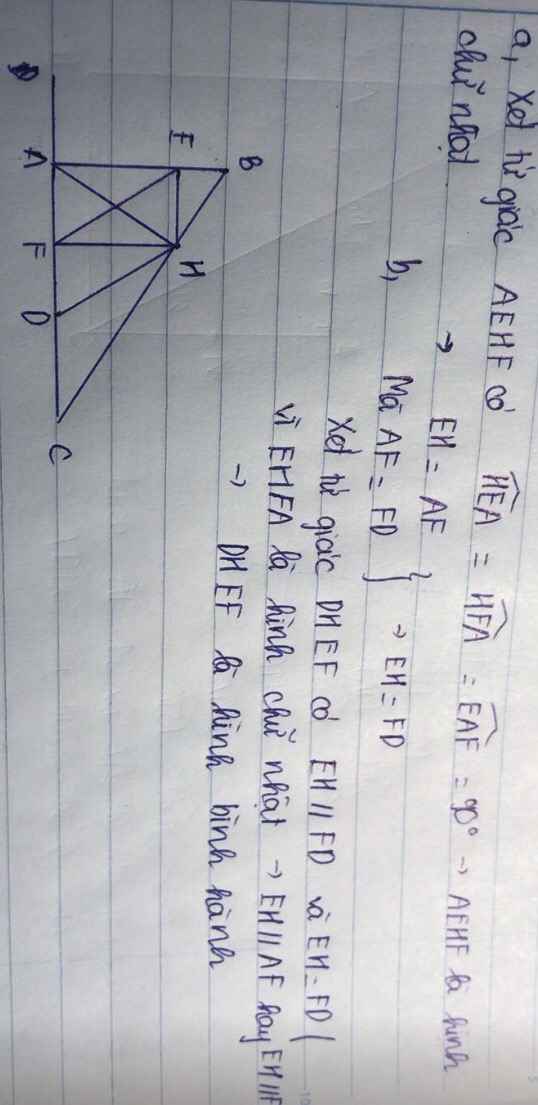
a, là hcn
câu b
từ câu a => hf // và = ae
mà hf = fm
=> fm // và = ae
=> đpcm
câu c
tam giác bnh có be vừa là dcao vừa trung tuyến
=> tam giác bnh cân b
=> bn=bh (1)
cmtt => ch=cm (2)
mà bc= bh+ch
=> bc^2 = (bh+ch+)^2
= bh^2 + 2 bh.ch +ch^2 (3)
(1) (2) (3) => ... (đpcm)
lười làm đầy đủ nên vắn ắt z thôi, thông cảm nhé ^_^