Cho tam giác ABC. P là một điểm bất kì trên BC. Gọi (I),(I1),(I2) lần lượt là đường tròn nội tiếp các tam giác ABC, AP B, AP C. EF là tiếp tuyến chung ngoài khác BC của (I1),(I2) (E ∈ (I1), F ∈ (I2)). Chứng minh rằng giao điểm của BE và CF luôn nằm trên đường tròn (I).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 11 2021
a) Gọi D,E,F lần lượt là tiếp điểm của (I;r) với MN,PQ,RS; T,U,V lần lượt là tiếp điểm của (I;r) với BC,AC,AB
Xét đường tròn (I;r) có hai tiếp tuyến tại D và U cắt nhau tại M \(\Rightarrow MD=MU\)(tính chất hai tiếp tuyến cắt nhau)
Tương tự, ta cũng có: \(SU=SF;\)\(RF=RT;\)\(QT=QE;\)\(PE=PV;\)\(NV=ND\)
Mà \(P_1=AM+AN+MN=AM+AN+MD+ND=AM+AN+MU+NV\)(1)
\(P_2=BP+BQ+PQ=BP+BQ+PE+QE=BP+BQ+PV+QT\)(2)
\(P_3=CS+CR+SR=CS+CR+SF+RF=CS+SR+RT+SU\)(3)
Từ (1), (2) và (3) \(\Rightarrow P_1+P_2+P_3=AM+AN+MU+NV+BP+BQ+PV+QT+CS+CR+RT+SU\)
\(=AM+AN+BP+BQ+CS+CR+\left(MU+SU\right)+\left(RT+QT\right)+\left(PV+NV\right)\)
\(=AM+AN+BP+BQ+CS+CR+MS+RQ+NP\)
\(=\left(AM+CS+MS\right)+\left(AN+BP+NP\right)+\left(BQ+QR+RC\right)\)
\(=AC+AB+BC=P\)
Vậy đẳng thức được chứng minh
VT
5 tháng 3 2019
Đáp án C
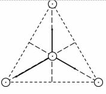
+ Từ hình vẽ ta có: 
+ 
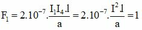N
+ Vì I 2 = 2I = 2 I 1 nên F 2 = 2 F 1 = 2 N
+ Vì I 3 = 3I = 3 I 1 nên F 3 = 3 F 1 = 3 N
+ 
N
+ Góc hợp giữa F 12 và F 2 được xác định như sau:
® j =
30
0
® Góc hợp giữa F 3 và F 12 là Dj = 150 0
+ 
N
Vậy đáp án C là gần nhất.
CM
24 tháng 1 2019
Chọn A.
(P1): y = f(x) = 1 4 x 2 - x có đỉnh I 2 (2;-1)
P(2): y = g(x) =
a
x
2
-
4
a
x
+
b
(a>0) 
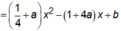
Duy ra I1, I2, I cùng nằm trên đường thẳng x = 2.
Mà giao điểm của (P1) và Ox là A(4;0) và B(0;0).
Suy ra tứ giác lồi AI1BI2 có hai đường chéo vuông góc và b – 4a >0
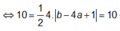
Tam giác IAB có diện tích là
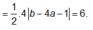
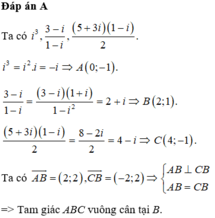
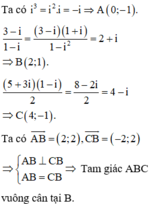
Gọi BC tiếp xúc với (I), (I1), (I2) lần lượt tại D,M,N. AP cắt EF tại H và tiếp xúc với (I1),(I2) lần lượt tại Q,R.
Ta có \(EF=MN;EF=HE+HF=2HQ+QR;MN=PM+PN=2PR+RQ\)
Suy ra \(HE=PN\)
Lại có \(DN=PD+PN=CD-CP+PN=\frac{CA+BC-AB+CP+PA-CA-2CP}{2}\)
\(=\frac{BP+PA-AB}{2}=PM\) hay \(PN=DM\). Suy ra \(HE=DM\)
Mà tứ giác EFNM là hình thang cân nên \(HD||EM||FN\)
Nếu gọi DH cắt lại (I) tại K thì các tam giác cân \(EI_1M,KID,FI_2N\) đồng dạng có các cạnh tương ứng song song đôi một
Do đó \(II_1,DM,KE\) đồng quy tại B, \(II_2,DN,KF\) đồng quy tại C
Nói cách khác, BE và CF cắt nhau tại K. Vậy BE và CF gặp nhau trên (I).