Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
THAM KHẢO
a) BK//OC, CK//OB.
Mà OB ^OC Þ OBKC là hình chữ nhật.
b)ABCD là hình thoi nên AB = BC. OBKC là hình chữ nhật nên KO =BC.
Þ KO = BC Þ ĐPCM.
c) nếu OBKC là hình vuông thì OB = OC Þ BD = AC. Vậy ABCD là hình vuông
a) BK//OC, CK//OB.
Mà OB ^OC Þ OBKC là hình chữ nhật.
b)ABCD là hình thoi nên AB = BC. OBKC là hình chữ nhật nên KO =BC.
Þ KO = BC Þ ĐPCM.
c) nếu OBKC là hình vuông thì OB = OC Þ BD = AC. Vậy ABCD là hình vuông
a: Xét tứ giác OBKC có
OB//KC
OC//BK
góc BOC=90 độ
Do đó: OBKC là hình chữ nhật
b: OBKC là hình chữ nhật
nên OK=BC
=>OK=AB
a) OBKC là hình bình hành (BK//OC,KC//OB) mà BOC=900 (vì BD _|_ AC do ABCD là hình thoi)
=>OBKC là hình chữ nhật
b) OBKC là hình chữ nhật (cmt) => OK=BC
mà BC=AB (ABCD là hình thoi)
=>AB=OK
c) Để hình chữ nhật OBKC là hình vuông <=> OB=OC
<=> AC=BD (vì OA=OC do O là tr.điểm AC trong hình thoi ABCD và OB=OC do O là tr.điểm BD)
Vậy hình thoi ABCD là hình vuông thì OBKC là hình vuông
nhầm chút,hình thoi ABCD có AC=BD thì OBKC là hình vuông nhé bn!
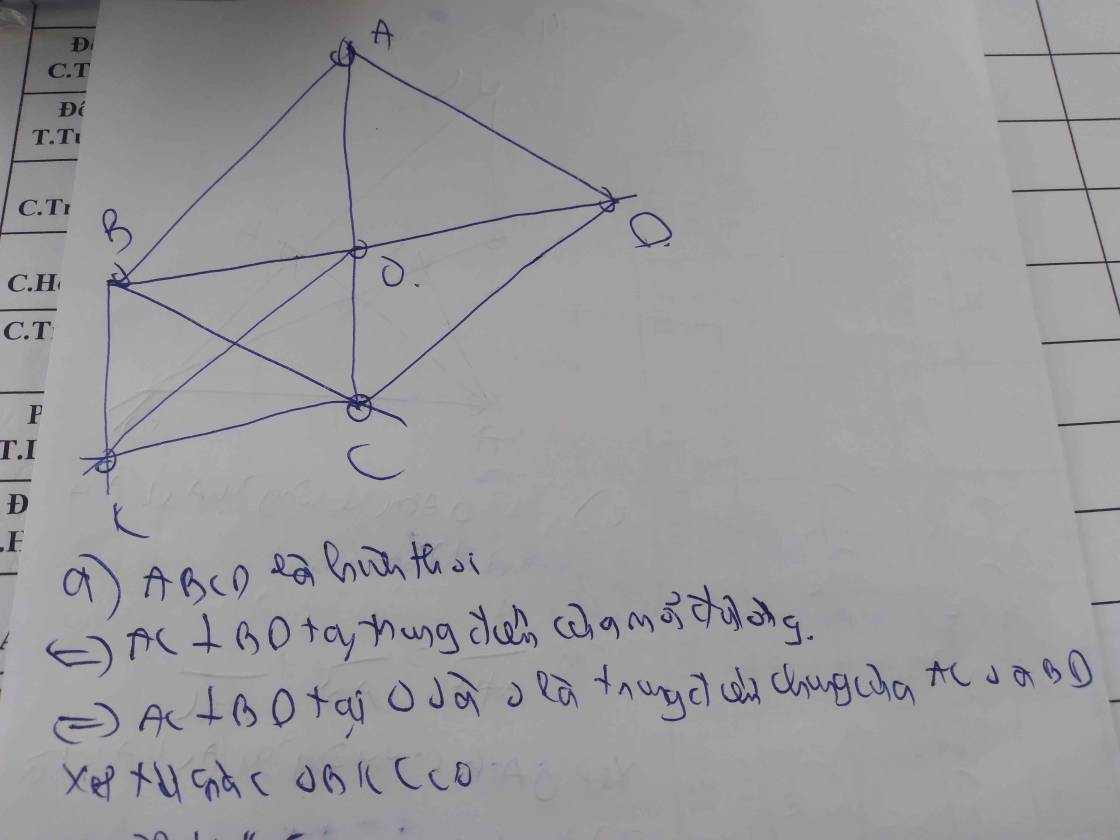
a) tứ giác OBKC có BK // AC (GT) hay BK // OC
CK // BD (gt) hay CK // BO
=> OBKC là HBH ( vì là tứ giác có các cạnh đối //)
^BOC = 90ĐỘ (T/C Hthoi)
=> OBKC là HCN (vì là HBH có 1 góc vuông)
b) OBKC là HCN => OK = BC (t/c HCN) (1)
ABCD là Hthoi (gt) => AB = BC (t/c Hthoi) (2)
từ (1) và (2) => OK = AB
c) Hthoi ABCD cần ĐK ^A = 90ĐỘ để OBKC là Hvuông