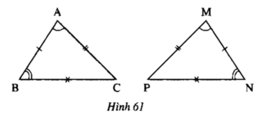
Quan sát hình 60a và 60b, các cạnh bằng nhau được đánh dấu bởi các kí hiệu giống nhau. Viết kí hiệu thể hiện sự bằng nhau của 2 tam giác có trên hình đó.(sách lớp 7 vnen trang 140)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 1 2019
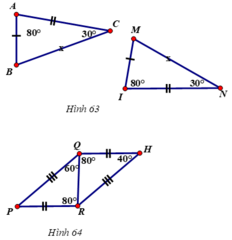
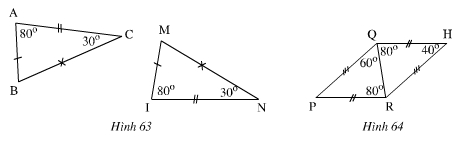
- Xem hình 63)
Ta có:
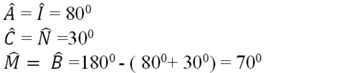
Và AB = MI; AC = IN; BC = MN
Nên ΔABC = ΔIMN
QUẢNG CÁO- Xem hình 64)
ΔPQR có:
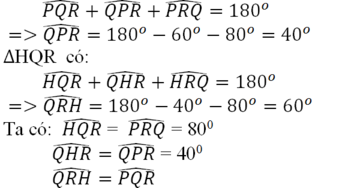
Và QH = RP, HR = PQ, QR cạnh chung
Nên ΔHQR = ΔPRQ
CM
23 tháng 5 2017
Hai tam giác bằng nhau vì có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau
kí hiệu: ΔABC = ΔMNP
21 tháng 9 2017
Hình 63
Ta có:
Và AB = MI; AC = IN; BC = MN
Nên ΔABC = ΔIMN
Hình 64 :
ΔPQR có:
Và QH = RP, HR = PQ, QR ( cạnh chung )
Nên ΔHQR = ΔPRQ
LH
20 tháng 4 2017
Xem hình a) ta có:
\(\widehat{A}=\widehat{I}=80^0\) ; \(\widehat{C}=\widehat{N}=30^0\)
\(\widehat{B}=\widehat{M}=180^0-\left(80^0+30^0\right)=70^0\)
Và AB=MI, AC=IN, BC=MN.
nên ∆ABC=∆IMN
Xem hình b) ta có:
\(\widehat{Q}_2=\widehat{R}_2=80^0\)=800 (ở vị trí so le trong)
Nên QH// RP
Nên \(\widehat{R}_1=\widehat{Q}_1\)= 600(so le trong)
\(\widehat{P}=\widehat{H}\)= 400
và QH= RP, HR= PQ, QR chung.
nên ∆HQR=∆PRQ.
15 tháng 8 2017
Xem hình a) ta có:
ˆAA^=ˆII^=800,ˆCC^=ˆNN^=300
ˆBB^=ˆMM^=1800-(800+300)=700
Và AB=MI, AC=IN, BC=MN.
nên ∆ABC=∆IMN
Xem hình b) ta có:
ˆQ2Q2^=ˆR2R2^=800 (ở vị trí so le trong)
Nên QH// RP
Nên ˆR1R1^ = ˆQ1Q1^= 600(so le trong)
ˆPP^=ˆHH^= 400
và QH= RP, HR= PQ, QR chung.
nên ∆HQR=∆PRQ.
28 tháng 10 2021
Bạn ơi, mik nhìn cái đề mà ko muốn đọc. Đọc xong rồi lại chả hiểu đề nó muốn nói gì. Bạn nên trình bày sao cho hợp lí và dễ hiểu, chứ nhìn như 1 mớ hỗn độn như thế này thì ai mà hiểu? Chưa kể hình thì ko có thì làm sao mà trả lời?
3 tháng 11 2016
tam giác ABC và tam giác HIK . vì AB = KI , góc B = góc K .
suy ra : AC=IH ; BC = KH
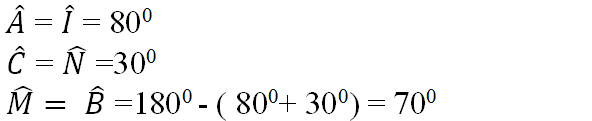
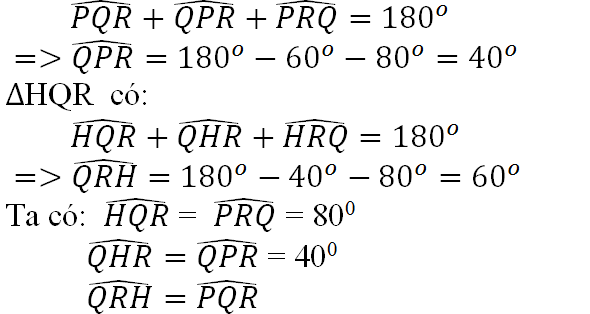
hình dâu hả bn
mk k có sách vnen
giup minh vs