Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB là tam giá đều nằm trong mặt phẳng vuông góc với đáy. Gọi M là trung điểm của SD, mặt phẳng (P) chứa CM và song song với BD cắt SB tại N, thể tích khối chóp S.CMN tính theo a bằng?
ai chỉ mk giải chi tiết với. thanks ạ ^^

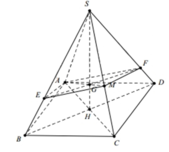

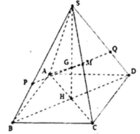
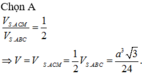
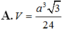
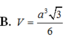
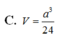
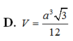
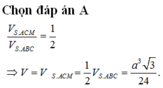
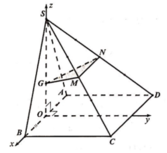
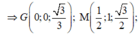
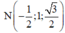
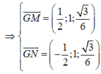
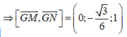
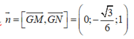
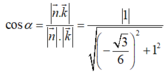
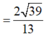
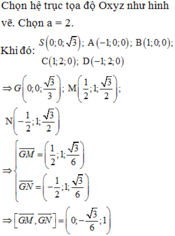
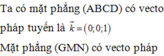

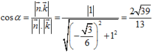
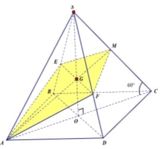
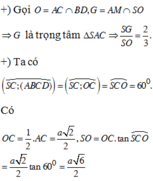

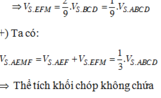
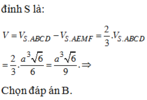
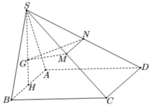


Hình bạn tự vẽ nha.
Xác định N: Qua M vẽ MN // BD (N thuộc SB)
Mà M là trung điểm SD → N là trung điểm SB
\(\frac{V_{S.CMN}}{V_{S.CDB}}=\frac{SM}{SD}\cdot\frac{SN}{SB}=\frac{1}{4}\) → VS.CMN = 1/4 * VS.CDB
Mà VS.CDB = 1/2 * VS.ABCD
→ VS.CDB = 1/8 * VS.ABCD
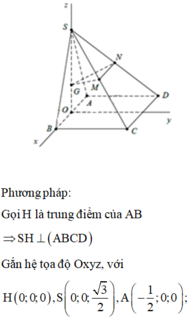
Gọi H là trung điểm AB → SH vg AB → SH vg (ABCD)\(V_{S.ABCD}=\frac{1}{3}\cdot SH\cdot S_{ABCD}=\frac{1}{3}\cdot\frac{a\sqrt{3}}{2}\cdot a^2=\frac{a^3\sqrt{3}}{6}\)
\(\Rightarrow V_{S.CMN}=\frac{1}{8}\cdot\frac{a^3\sqrt{3}}{6}\)
c.ơn bạn nhiều nha :)