Cho các hàm số \(y=f\left(x\right)=2x\) và \(y=g\left(x\right)=\frac{18}{x}\). Không vẽ đồ thị của chúng, em hãy tính tọa độ giao điểm của 2 đồ thị, sau đó rút ra nhận xét về phương pháp chung để tìm tọa độ giao điểm của 2 đồ thị hàm số.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
T
13 tháng 6 2019
Phương trình hoàn độ và giao điểm của hai đồ thị hàm số trên là:
\(2x=\frac{18}{x}\left(x\ne0\right)\Leftrightarrow2x^2-18=0\)
\(\Leftrightarrow2\left(x^2-9\right)=0\Leftrightarrow\orbr{\begin{cases}x=3\\x=-3\end{cases}}\) (T/M)
Với x = 3 thì y = 6 ta được A = (3;6)
Với x = -3 thì y = -6 ta được B = (-3;-6)
Vậy tọa độ giao điểm của hai đồ thị hàm số trên là A = (3;6) và B = (-3;-6)
11 tháng 7 2017
Hoành độ giao điểm 2 đồ thị là nghiệm của phương trình \(2x=\frac{18}{x}\Rightarrow2x^2=18\Rightarrow x^2=9\Rightarrow\orbr{\begin{cases}x=3\\x=-3\end{cases}}\)
Với \(x=3\Rightarrow y=6\Rightarrow A\left(3;6\right)\)
Với \(x=-3\Rightarrow y=-6\Rightarrow B\left(-3;-6\right)\)
Vậy 2 giao điểm là \(A\left(3;6\right);B\left(-3;-6\right)\)
15 tháng 4 2021
Câu 2:
c) Phương trình hoành độ giao điểm của (P) và (d) là:
\(\dfrac{1}{2}x^2=2x+6\)
\(\Leftrightarrow\dfrac{1}{2}x^2-2x-6=0\)
\(\Leftrightarrow x^2-4x-12=0\)
\(\Leftrightarrow x^2-4x+4=16\)
\(\Leftrightarrow\left(x-2\right)^2=16\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=4\\x-2=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=6\\x=-2\end{matrix}\right.\)
Thay x=6 vào (P), ta được:
\(y=\dfrac{1}{2}\cdot6^2=18\)
Thay x=-2 vào (P), ta được:
\(y=\dfrac{1}{2}\cdot\left(-2\right)^2=\dfrac{1}{2}\cdot4=2\)
Vậy: Tọa độ giao điểm của (P) và (d) là (6;18) và (-2;2)
15 tháng 4 2021
Câu 3:
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-b}{a}=\dfrac{-\left(-2\right)}{1}=2\\x_1\cdot x_2=\dfrac{c}{a}=\dfrac{-1}{1}=-1\end{matrix}\right.\)
Ta có: \(P=x_1^3+x_2^3\)
\(=\left(x_1+x_2\right)^3-3\cdot x_1x_2\left(x_1+x_2\right)\)
\(=2^3-3\cdot\left(-1\right)\cdot2\)
\(=8+3\cdot2\)
\(=8+6=14\)
Vậy: P=14
NT
0
12 tháng 9 2023
a)
- Với \(x = - 2 \Rightarrow f\left( { - 2} \right) = - 2;g\left( { - 2} \right) = - 2 + 3 = 1\);
- Với \(x = - 1 \Rightarrow f\left( { - 1} \right) = - 1;g\left( { - 1} \right) = - 1 + 3 = 2\);
- Với \(x = 0 \Rightarrow f\left( 0 \right) = 0;g\left( 0 \right) = 0 + 3 = 3\);
- Với \(x = 1 \Rightarrow f\left( 1 \right) = 1;g\left( 1 \right) = 1 + 3 = 4\);
- Với \(x = 2 \Rightarrow f\left( 2 \right) = 2;g\left( 2 \right) = 2 + 3 = 5\);
Ta có bảng sau:
\(x\) | –2 | –1 | 0 | 1 | 2 |
\(y = f\left( x \right) = x\) | –2 | –1 | 0 | 1 | 2 |
\(y = g\left( x \right) = x + 3\) | 1 | 2 | 3 | 4 | 5 |
b)
- Vẽ đồ thị hàm số \(y = f\left( x \right) = x\)
Cho \(x = 1 \Rightarrow y = f\left( x \right) = 1\). Ta vẽ điểm \(A\left( {1;1} \right)\)
Đồ thị hàm số \(y = x\) là đường thẳng đi qua điểm \(O\left( {0;0} \right)\) và \(A\left( {1;1} \right)\).
- Các điểm có tọa độ thỏa mãn hàm số \(y = g\left( x \right)\) trong bảng trên là \(B\left( { - 2;1} \right);C\left( { - 1;2} \right);D\left( {0;3} \right);E\left( {1;4} \right);F\left( {2;5} \right)\).
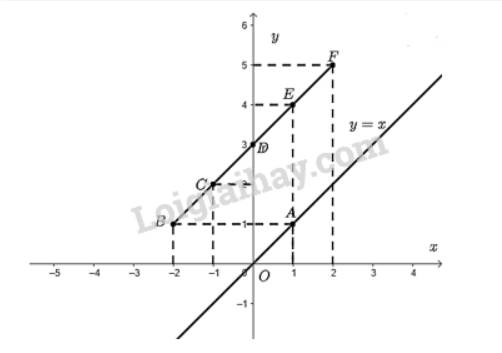
c) Ta đặt thước thẳng kiểm tra thì thấy các điểm thuộc đồ thị hàm số \(y = g\left( x \right) = x = 3\) thẳng hàng với nhau.
Dự đoán cách vẽ đồ thị hàm số \(y = g\left( x \right)\):
Bước 1: Chọn hai điểm \(A;B\) phân biệt thuộc đồ thị hàm số \(y = g\left( x \right)\).
Bước 2: Vẽ đường thẳng đi qua hai điểm \(A;B\).
Đồ thị hàm số \(y = g\left( x \right)\) là đường thẳng đi qua hai điểm \(A;B\).
Gọi A (xo; yo) là giao điểm của hai đồ thị
A \(\in\) đồ thị hàm số y = 2x => yo = 2xo
A \(\in\) đồ thị hàm số y = 18/x => yo = 18/xo
=> 2xo = 18/xo => 2xo2 = 18 <=> x2o = 9 => xo = 3 hoặc xo = - 3
+) xo = 3 => yo = 6 => A (3;6)
+) xo = -3 => yo = - 6 => A (-3; -6)
Vậy...
* Nhận xét: Để tìm tọa độ giao điểm của hai đồ thị hàm số
- Tìm hoành độ giao điểm :Giải f(x) = g(x) => x = ....
- Thay x tìm được vào hàm số y = f(x) hoặc y = g(x) => y =...