một ô tô chuyển động biến đổi đều , trong giây cuối cùng ( trước khi dừng hẳn) đi được 0,5 m. Tính gia tốc
ĐS a=-1
mọi người giúp mình làm với thanks nhìu ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 10 2021
Ta có: \(\left\{{}\begin{matrix}v=v_0+at\\S=v_0t+\dfrac{1}{2}at^2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}0=v_0+a\cdot5\\3,125=v_0\cdot5+\dfrac{1}{2}\cdot a\cdot5^2\end{matrix}\right.\)
\(\Rightarrow\) \(v_0=1,25\)m/s và \(a=-0,25\) m/s2
VT
30 tháng 6 2017
Đáp án A.
Xét bài toán tổng quát: Một vật chuyển động thẳng chậm dần đều với gia tốc a. Tính quãng đường vật đi được trong n giây cuối trước khi vật dừng hẳn.
Giả sử chọn chiều dương là chiều chuyển động của vật. Gốc thời gian là lúc vật bắt đầu chuyển động.
Gọi t là thời gian để vật đi toàn bộ quãng đường s đến khi vật dừng hẳn thì:
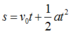
Quãng đường vật đi được trong ( t – n ) giây đầu là:
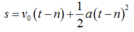
Vậy quãng đường vật đi được trong n giây cuối cùng trước khi dừng hẳn là:
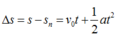
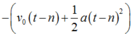
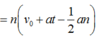
Mà khi vật dừng lại thì 
Vậy ta có
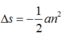
Lưu ý: Do ∆ s >0 nên a<0 , phù hợp với tính chất của chuyển động chậm dần đều khi chọn chiều dương là chiều chuyển động thì .
Khi vật chuyển động chậm dần đều, quãng đường vật đi được trong n giây cuối trước khi vật dừng hẳn là:
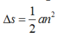
Áp dụng vào bài toán:
CM
2 tháng 2 2017
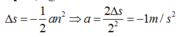
Đáp án C
Thời gian ô tô phanh đến khi dừng hẳn là t = 10 s
Do đó s = 20.5 + ∫ 0 10 − 2 t + 20 d t = 100 + 20 t − t 2 = 0 10 200 m
HD
Hà Đức Thọ
Admin
19 tháng 8 2016
Gọi vận tốc ban đầu là \(v_0\), vận tốc sau 5s là \(v_1\), ta có:
\(0=v_0-a.t\Rightarrow v_0=a.t=10.a\)
\(v_1=v_0-a.t'=10.a-a.5=5a\)
Áp dụng công thức độc lập:
\(v_1^2-v_0^2=2aS\)
\(\Rightarrow (5a)^2-(10a)^2=2a.37,5\)
Giải PT rồi tìm gia tốc a nhé.
NCC
chọn gốc thời gian to là 1s trước khi xe dừng
gốc tọa độ là vị trí tại thời điểm to
chiều dương là chiều vật chuyển động. ta có ptcđ của vật trong 1s cuối là
x = xo + vo.t + \(\dfrac{at^2}{2}\)
=> 0,5 = vo.1 + \(\dfrac{a.1^2}{2}\) = vo + \(\dfrac{a}{2}\) => vo = 0,5 - \(\dfrac{a}{2}\) (1)
lại có : v2 - vo2 = 2aΔx =>02- vo2 = 2a.0,5 => 0- vo2 = a =>vo2 = -a (2)
từ 1 và 2 ta có hpt : \(\left\{{}\begin{matrix}v_0=0,5-\dfrac{a}{2}\\v_0^2=-a\end{matrix}\right.\)
giải ra ta có a = -1