Cho hình vuông ABCD có chu vi 16m. Lần lượt lấy A, B, C, D làm tâm vẽ các đường tròn bán kính bằng 1/2 cạnh hình vuông, cắt các cạnh của hình vuông lần lượt tại các điểm M, N, P, Q. Tính diện tích phần gạch chéo. A B D C M N P Q giúp mình nhanhớ vẽ hình nữa nha cố gắng giúp mk...
Đọc tiếp
Cho hình vuông ABCD có chu vi 16m. Lần lượt lấy A, B, C, D làm tâm vẽ các đường tròn bán kính bằng 1/2 cạnh hình vuông, cắt các cạnh của hình vuông lần lượt tại các điểm M, N, P, Q. Tính diện tích phần gạch chéo.
giúp mình nha
nhớ vẽ hình nữa nha cố gắng giúp mk vs
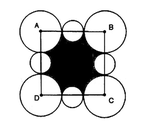
Cạnh của hình vuông \(ABCD\) bằng:
\(16\div4=4\left(cm\right)\)
Các hình \(AQM;BMN;CNP;DPQ\) có diện tích bằng \(\frac{1}{4}\) diện tích hình tròn có bán kính bằng:
\(4\div2=2\left(cm\right)\)
Tổng diện tích của 4 hình trên bằng diện tích của hình tròn bán kính 2cm.
Diện tích hình vuông \(ABCD\):
\(4\times4=16\left(cm^2\right)\)
Diện tích hình tròn bán kính 2cm bằng:
\(2\times2\times3,14=12,56\left(cm\right)\)
Diện tích phần gạch chéo bằng diện tích hình vuông \(ABCD\) trừ đi diện tích hình tròn bán kính 2cm.
Diện tích phần gạch chéo bằng:
\(16-12,56=3,44\left(cm^2\right)\)
Đáp số: \(3,44cm^2\)
mk vẽ hình bj sai cái hình ở trong đáng lẽ cái đường thẳng phải cong giống đường tròn nhưng mk vẽ mãi nó chả đc